题目内容
7.已知函数f(x)=ex-ax2-bx-1,其中a、b∈R,e=2.71828…为自然对数的底数.设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值.分析 由f(x)求导得g(x)=f′(x)=ex-2ax-b,再求导得g′(x)=ex-2a,从而讨论a以确定导数的正负,从而确定函数在区间[0,1]上的单调性,由单调性确定最小值点及最小值即可.
解答 解:∵f(x)=ex-ax2-bx-1,
∴g(x)=f′(x)=ex-2ax-b.
所以g′(x)=ex-2a.
当x∈[0,1]时,g′(x)∈[1-2a,e-2a].
当a≤$\frac{1}{2}$时,g′(x)≥0,所以g(x)在[0,1]上单调递增.
因此g(x)在[0,1]上的最小值是g(0)=1-b;
当a≥$\frac{e}{2}$时,g′(x)≤0,所以g(x)在[0,1]上单调递减,
因此g(x)在[0,1]上的最小值是g(1)=e-2a-b;
当$\frac{1}{2}$<a<$\frac{e}{2}$时,令g′(x)=0得x=ln(2a)∈(0,1).
所以函数g(x)在区间[0,ln(2a)]上单调递减,在区间(ln(2a),1]上单调递增.
于是,g(x)在[0,1]上的最小值是g(ln(2a))=2a-2aln(2a)-b;
综上所述,
当a≤$\frac{1}{2}$时,g(x)在[0,1]上的最小值是g(0)=1-b;
当$\frac{1}{2}$<a<$\frac{e}{2}$时,g(x)在[0,1]上的最小值是g(ln(2a))=2a-2aln(2a)-b;
当a≥$\frac{e}{2}$时,g(x)在[0,1]上的最小值是g(1)=e-2a-b.
点评 本题考查了导数的综合应用,同时考查了分类讨论的数学思想应用,属于中档题.

练习册系列答案
相关题目
12.已知抛物线x2=4y,过点P(0,2)作斜率分别为k1,k2的直线l1,l2,与抛物线分别交于两点,若k1k2 =-$\frac{3}{4}$,则四个交点构成的四边形面积的最小值为( )
| A. | 18$\sqrt{3}$ | B. | 20$\sqrt{3}$ | C. | 22$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
 ”的否定是“
”的否定是“ ”;
”; 是空间中的三条直线,
是空间中的三条直线, 的充要条件是
的充要条件是 且
且 ;
; 中,若
中,若 ,则
,则 ”的逆命题为假命题;
”的逆命题为假命题; ,有
,有 ,且当
,且当 时,
时, ,则当
,则当 时,
时, .
. 的离心率为
的离心率为 ,以
,以 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. 的标准方程;
的标准方程; ,和面内一点
,和面内一点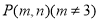 ,过点
,过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若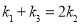 ,试求
,试求 满足的关系式.
满足的关系式.