题目内容
已知定义在R上的函数f(x)满足f(x+1)=-f(x)。当x [0,1]时,f(x)=
[0,1]时,f(x)= -x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
-x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
A.(- , , ) ) | B.(- , , ] ] | C. | D.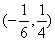 |
B
解析试题分析:根据题意,可求出f(x)区间(-1,2]上的分段函数的表达式,然后在同一坐标系内作出y=f(x)和y=m(x+1)的图象,观察直线y=m(x+1)的斜率m变化,可得直线y=m(x+1)位于图中AB、AC之间(包括AC)活动时,两个图象有三个公共点,由此求出直线AB、AC的斜率并与实数m加以比较,即可得到本题的答案.解:设得x+1∈[0,1],此时f(x+1)= -(x+1)=-x-
-(x+1)=-x- ,
,
∵函数f(x)满足f(x+1)=-f(x)
∴当-1≤x≤0时,f(x)=x+ .又∵f(x+2)=-f(x+1)═-[f(-x)]=f(x)∴f(x)是以2为周期的函数,可得当1≤x≤2时,f(x)=f(x-2)=x-
.又∵f(x+2)=-f(x+1)═-[f(-x)]=f(x)∴f(x)是以2为周期的函数,可得当1≤x≤2时,f(x)=f(x-2)=x- 综上所述,得f(x)区间(-1,2]上的表达式为f(x)=
综上所述,得f(x)区间(-1,2]上的表达式为f(x)= ,
,
为了研究g(x)=f(x)-m(x+1)在区间(-1,2]上的零点,将其形为,f(x)=m(x+1),在同一坐标系内作出y=f(x)和y=m(x+1)的图象,如右图所示,y=f(x)图象是三条线段构成的折线,y=m(x+1)的图象是直线,因为直线y=m(x+1)经过定点A(-1,0),所以由图象可得当直线y=m(x+1),位于图中AB、AC之间(包括AC)活动时,两个图象有三个公共点,相应地,g(x)=f(x)-m(x+1)在区间(-1,2]也有3个零点,∵B(1,-0.5),C(2,0.5),,∴kAB=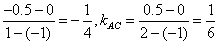 而直线y=m(x+1)的斜率为m,它在AB、AC之间(包括AC)活动时,m(
而直线y=m(x+1)的斜率为m,它在AB、AC之间(包括AC)活动时,m(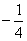 ,
, ].因此,使得g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点的m取值范围为m(
].因此,使得g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点的m取值范围为m(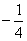 ,
, ],故选B
],故选B
考点:分段函数图象
点评:本题给出分段函数图象与直线有三个公共点,求直线斜率m的取值范围,着重考查了基本初等函数的图象与性质、直线的斜率及其变化等知识,属于中档题

 阅读快车系列答案
阅读快车系列答案若 ,且
,且 ,则函数
,则函数 ( )
( )
A.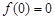 且 且 为奇函数 为奇函数 | B.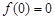 且 且 为偶函数 为偶函数 |
C. 为增函数且为奇函数 为增函数且为奇函数 | D. 为增函数且为偶函数 为增函数且为偶函数 |
已知函数 是定义域为
是定义域为 的偶函数,且
的偶函数,且 ,若
,若 在
在 上是减函数,那么
上是减函数,那么 在
在 上是 ( )
上是 ( )
| A.增函数 | B.减函数 | C.先增后减的函数 | D.先减后增的函数 |
函数 在区间
在区间 上( )
上( )
| A.没有零点 | B.只有一个零点 | C.有两个零点 | D.以上选项都错误 |
设点 在曲线
在曲线 上,点
上,点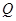 在曲线
在曲线 上,则
上,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
已知函数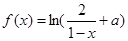 (
( 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( )
| A.1 | B.—3 | C.3 | D.—1 |

 ,则
,则 的大致图象是( )
的大致图象是( )