题目内容
已知函数 是定义域为
是定义域为 的偶函数,且
的偶函数,且 ,若
,若 在
在 上是减函数,那么
上是减函数,那么 在
在 上是 ( )
上是 ( )
| A.增函数 | B.减函数 | C.先增后减的函数 | D.先减后增的函数 |
A
解析试题分析:由偶函数的性质可以得出[0,1]上的单调性,再由 可得出函数的周期是2,由此两个性质即可研究出函数在[2,3]上的单调性.解:由题意
可得出函数的周期是2,由此两个性质即可研究出函数在[2,3]上的单调性.解:由题意 ,故有
,故有 = f(x-1)所以函数的周期是2,又函数f(x)是定义域为R的偶函数且在[-1,0]上是减函数,故在[0,1]上增,由上性质知,f(x)在[2,3]上的单调性与在[0,1]上的单调性相同,故f(x)在[2,3]上是增函数,故选A
= f(x-1)所以函数的周期是2,又函数f(x)是定义域为R的偶函数且在[-1,0]上是减函数,故在[0,1]上增,由上性质知,f(x)在[2,3]上的单调性与在[0,1]上的单调性相同,故f(x)在[2,3]上是增函数,故选A
考点:函数的奇偶性与单调性
点评:本题考查函数的奇偶性与单调性的综合,此类题是函数性质考查中的一个比较重要的类型,求解本题的关键是正确理解函数的性质并能熟练运用这些性质做出判断,本题根据恒等式得出函数的周期性是对函数周期性考查的一种比较新颖的方法.本题易因对恒等式理解不透未能得出周期而导致解题失败.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如下图是函数 的大致图象,则
的大致图象,则 等于
等于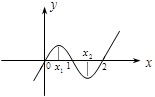
A.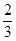 | B. |
C. | D. |
函数 的值域为( )
的值域为( )
A. | B. | C.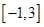 | D. |
函数 的反函数是( )
的反函数是( )
A. | B. |
C. | D. |
函数 有两个不同的零点,则实数
有两个不同的零点,则实数 的取值范围是
的取值范围是
A. | B. |
C.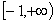 | D. |
已知方程 在
在 有两个不同的解
有两个不同的解 (
( ),则下面结论正确的是:
),则下面结论正确的是:
A. | B. |
C. | D. |
已知定义在R上的函数f(x)满足f(x+1)=-f(x)。当x [0,1]时,f(x)=
[0,1]时,f(x)= -x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
-x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
A.(- , , ) ) | B.(- , , ] ] | C. | D.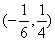 |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
| A.向右平移1个单位再向上平移1个单位 |
| B.向左平移1个单位再向上平移1个单位 |
| C.向左平移1个单位再向下平移1个单位 |
| D.向右平移1个单位再向下平移1个单位 |
 的图象如左图,那么导函数
的图象如左图,那么导函数 的图象可能是( )
的图象可能是( )
