题目内容
阅读下面材料:
根据两角和与差的正弦公式,有
 ------①
------①
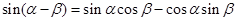 ------②
------②
由①+② 得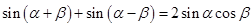 ------③
------③
令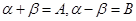 有
有
代入③得
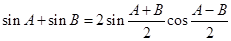 .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:
 ;
;
(Ⅱ)若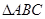 的三个内角
的三个内角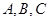 满足
满足 ,试判断
,试判断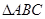 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
【答案】
(1)结合两角和的余弦公式来联立方程组来求解得到。
(2)直角三角形
【解析】
试题分析:解法一:(Ⅰ)因为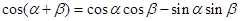 , ①
, ①
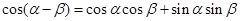 , ②
2分
, ②
2分
①-② 得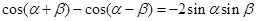 . ③
3分
. ③
3分
令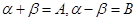 有
有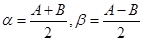 ,
,
代入③得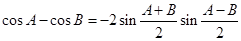 .
6分
.
6分
(Ⅱ)由二倍角公式,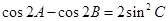 可化为
可化为
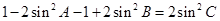 ,
8分
,
8分
即 .
9分
.
9分
设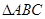 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为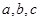 ,
,
由正弦定理可得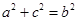 .
11分
.
11分
根据勾股定理的逆定理知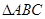 为直角三角形.
12分
为直角三角形.
12分
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的结论和二倍角公式, 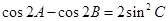 可化为
可化为
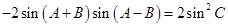 ,
8分
,
8分
因为A,B,C为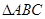 的内角,所以
的内角,所以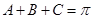 ,
,
所以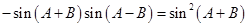 .
.
又因为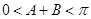 ,所以
,所以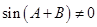 ,
,
所以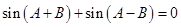 .
.
从而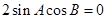 .
10分
.
10分
又因为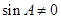 ,所以
,所以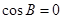 ,即
,即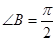 .
.
所以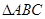 为直角三角形. 12分
为直角三角形. 12分
考点:两角和与差三角函数公式、二倍角公式
点评:本小题主要考查两角和与差三角函数公式、二倍角公式、三角函数的恒等变换等基础知识,考查推理论证能力,运算求解能力,考查化归与转化思想等

练习册系列答案
相关题目
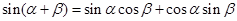 ------①
------①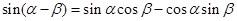 ------②
------②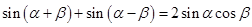 ------③
------③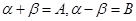 有
有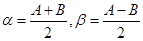
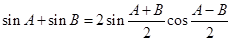 .
.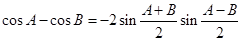 ;
;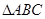 的三个内角
的三个内角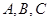 满足
满足 ,直接利用阅读材料及(1)中的结论试判断
,直接利用阅读材料及(1)中的结论试判断