题目内容
下列各组函数中,定义域相同的一组是
- A.y=ax与y=logax(a>0,且a≠1)
- B.y=x与

- C.y=lgx与
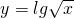
- D.y=x2与y=lgx2
C
分析:先判断两个函数的定义域是否是同一个集合,再判断两个函数的定义域是否可以化为一致.
解答:A、∵y=ax的定义域为R,y=logax的定义域为(0,+∞).∴定义域不相同;
B、∵y=x的定义域为R, 的定义域为[0,+∞).∴定义域不相同;
的定义域为[0,+∞).∴定义域不相同;
C、∵y=lgx的定义域为(0,+∞),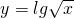 的定义域为(0,+∞).∴定义域相同;
的定义域为(0,+∞).∴定义域相同;
D、y=x2的定义域为R,y=lgx2的定义域为(-∞,0)∪(0,+∞),∴定义域不相同;
故选C.
点评:本题主要考查函数的概念,函数的定义域及其求法,解答关键是看两个函数的定义域是否同一个集合,属于基础题.
分析:先判断两个函数的定义域是否是同一个集合,再判断两个函数的定义域是否可以化为一致.
解答:A、∵y=ax的定义域为R,y=logax的定义域为(0,+∞).∴定义域不相同;
B、∵y=x的定义域为R,
 的定义域为[0,+∞).∴定义域不相同;
的定义域为[0,+∞).∴定义域不相同;C、∵y=lgx的定义域为(0,+∞),
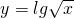 的定义域为(0,+∞).∴定义域相同;
的定义域为(0,+∞).∴定义域相同;D、y=x2的定义域为R,y=lgx2的定义域为(-∞,0)∪(0,+∞),∴定义域不相同;
故选C.
点评:本题主要考查函数的概念,函数的定义域及其求法,解答关键是看两个函数的定义域是否同一个集合,属于基础题.

练习册系列答案
相关题目
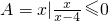 ,
,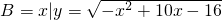 ,则A∩B等于
,则A∩B等于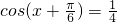 ,求
,求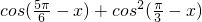 的值;
的值;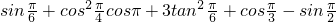 .
. (n∈N*),则
(n∈N*),则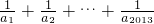 等于________.
等于________.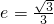 ,直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切.
,直线l:y=x+2与以原点为圆心,椭圆C的短半轴为半径的圆O相切.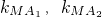 ,证明
,证明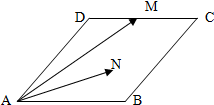 如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则
如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则 的最大值为
的最大值为
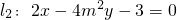 垂直,求直线l1的方程;
垂直,求直线l1的方程;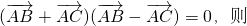 △ABC为
△ABC为