题目内容
9.给出下列四个命题,其中正确命题的序号是( )①已知f(x)=x2+bx+c是偶函数,则b=0
②若函数f(x)的值域为[0,2],则函数f(2x)的值域为[0,2]
③若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
④已知集合P={a,b},Q={-1,0,1}则映射f:P→Q中满足f(b)=0的映射共有3个.
⑤如果二次函数y=3x2+2(a-1)x+b在区间(-∞,1]上是减函数,那么a的取值范围是a≤-2.
| A. | ①②⑤ | B. | ①②④⑤ | C. | ①②③⑤ | D. | ①③④⑤ |
分析 ①利用偶函数的性质可得:f(-x)=f(x),化为2bx=0,对于任意实数x都成立,则b=0,即可判断出正误;
②由函数f(x)的值域为[0,2],则函数f(2x)的值域没有改变,即可判断出正误;
③由函数f(x)的定义域为[0,2],由0≤2x≤2,解得x即可得出函数f(2x)的定义域为,即可判断出正误;
④映射f:P→Q中满足f(b)=0的映射为:f(b)=0,f(a)=0,-1,1,共有3个,即可判断出正误.
⑤利用二次函数的单调性可得:1≤$-\frac{2(a-1)}{3×2}$,解得a范围,即可判断出正误.
解答 解:对于①,∵f(x)=x2+bx+c是偶函数,∴f(-x)=f(x),化为2bx=0,对于任意实数x都成立,则b=0,正确;
对于②,若函数f(x)的值域为[0,2],则函数f(2x)的值域没有改变,仍然为[0,2],正确;
对于③,若函数f(x)的定义域为[0,2],由0≤2x≤2,解得0≤x≤1,则函数f(2x)的定义域为[0,1],因此不正确;
对于④,集合P={a,b},Q={-1,0,1},则映射f:P→Q中满足f(b)=0的映射为:f(b)=0,f(a)=0,-1,1,共有3个,正确.
对于⑤,如果二次函数y=3x2+2(a-1)x+b在区间(-∞,1]上是减函数,则1≤$-\frac{2(a-1)}{3×2}$,解得a≤-2.那么a的取值范围是a≤-2.因此正确.
综上可知:正确的为①②④⑤.
故选:B.
点评 本题考查了函数的单调性与奇偶性、定义域与值域等性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
20.在四棱锥P-ABCD中,PD⊥底面ABCD,四边形ABCD为正方形,且PD=AB=1,$\overrightarrow{BG}$=$\frac{1}{3}$$\overrightarrow{BD}$,则$\overrightarrow{PG}$与底面ABCD的夹角的正弦值为( )
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{3\sqrt{17}}{17}$ | C. | -$\frac{2\sqrt{34}}{17}$ | D. | -$\frac{3\sqrt{17}}{17}$ |
1.若a=i+i2+…+i2013(i是虚数单位),则$\frac{a(1+a)^{2}}{1-a}$的值为( )
| A. | i | B. | 1-i | C. | -1+i | D. | -1-i |
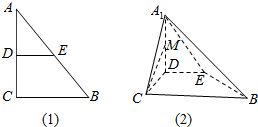 如图(1),在Rt△ABC中,∠C=90°,BC=2,AC=4,点D,E分别是AC,AB的中点,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC如图(2)所示,M为A1D的中点,求CM与面A1EB所成角的正弦值.
如图(1),在Rt△ABC中,∠C=90°,BC=2,AC=4,点D,E分别是AC,AB的中点,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC如图(2)所示,M为A1D的中点,求CM与面A1EB所成角的正弦值.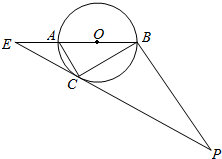 如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.
如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.