题目内容
(本题满分14分,第1小题6分,第2小题8分)
已知函数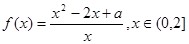 ,其中常数a > 0.
,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在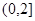 上是减函数;
上是减函数;
(2) 求函数f(x)的最小值.
【答案】
(1)任取0<x1<x2≤2,则f(x1)–f(x2)=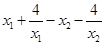
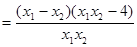 ,
,
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2);
(2)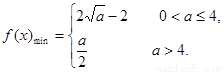 。
。
【解析】
试题分析:(1) 当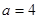 时,
时,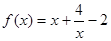 ,…………………………………………1分
,…………………………………………1分
任取0<x1<x2≤2,则f(x1)–f(x2)=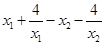
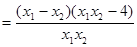 ………………3分
………………3分
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2)………………………………………5分
所以函数f(x)在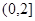 上是减函数;………………………………………………………6分
上是减函数;………………………………………………………6分
(2)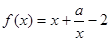
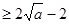 ,……………………………………………………7分
,……………………………………………………7分
当且仅当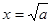 时等号成立,…………………………………………………………8分
时等号成立,…………………………………………………………8分
当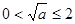 ,即
,即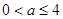 时,
时,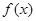 的最小值为
的最小值为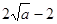 ,………………………10分
,………………………10分
当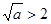 ,即
,即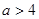 时,
时,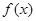 在
在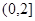 上单调递减,…………………………………11分
上单调递减,…………………………………11分
所以当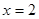 时,
时,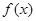 取得最小值为
取得最小值为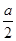 ,………………………………………………13分
,………………………………………………13分
综上所述: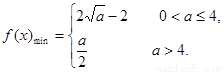 ………………………………………14分
………………………………………14分
考点:函数的单调性和最值;基本不等式。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。

练习册系列答案
相关题目

 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1. ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
 ,若不等式
,若不等式 的解集为
的解集为 。
。 的值;
的值; 在
在 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。