题目内容
已知函数f(x)=px- -2lnx、
-2lnx、(Ⅰ)若p=3,求曲f9想)在点(1,f(1))处的切线方程;
(Ⅱ)若p>0且函f(x)在其定义域内为增函数,求实数p的取值范围;
(Ⅲ)若函数y=f(x)在x∈(0,3)存在极值,求实数p的取值范围.
【答案】分析:(I)把p=3代入f(x)中确定出解析式,求出f(1)确定出切点坐标和导函数,把x=1代入导函数中求出的导函数值即为切线方程的斜率,根据切点坐标和斜率写出切线方程即可;
(Ⅱ)求出f(x)的导函数,要使函数在定义域内位增函数,即要导函数在定义域内恒大于0,由导函数的分子解出p大于等于一个关系式,利用基本不等式求出这个关系式的最大值,进而得到p的取值范围;
(Ⅲ)求出f(x)的导函数,令导函数等于0得到一个方程,记作(*),设方程的左边为函数h(x),当p=0时求出方程(*)的解为0,显然函数无极值点;当p不为0时,讨论函数有一个极值和两个极值,列出不等式组,求出不等式组的解集即可得到p的取值范围.
解答:解:(I)当p=3时,函数f(x)=3x-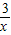 -2lnx,
-2lnx,
f(1)=3-3-2ln1=0,f′(x)=3-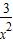 -
-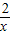 ,
,
曲线f(x)在点(1,f(x))处的切线的斜率为f′(1)=3-3-2=4,
∴f(x)在点(1,f(x))处得切线方程为y-0=4(x-1),即y=4x-4;
(Ⅱ)f′(x)=p+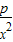 -
-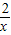 =
=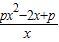 ,(4分)
,(4分)
要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0在(0,+∞)内恒成立,
即px2-2x+p≥0在(0,+∞)上恒成立,(5分)
即p≥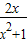 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
设M(x)=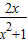 ,(x>0)(6分)
,(x>0)(6分)
则M(x)=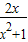 =
=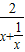 ,
,
∵x>0,∴x+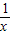 ≥2,当且仅当x=1时取等号,(7分)
≥2,当且仅当x=1时取等号,(7分)
∴M(x)≤1,即M(x)max=1,∴p≥1,
所以实数p的取值范围是[1,+∞);(8分)
(Ⅲ)∵f′(x)= ,令f′(x)=0,即px2-2x+p=0(*)(9分)
,令f′(x)=0,即px2-2x+p=0(*)(9分)
设h(x)=px2-2x+p,x∈(0,3),
当p=0时,方程(*)的解为x=0,此时f(x)在x∈(0,3)无极值,所以p≠0;
当p≠0时,h(x)=px2-2x+p的对称轴方程为x=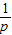 ,
,
①若f(x)在x∈(0,3)恰好有一个极值,
则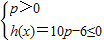 或
或 ,解得:0<p≤
,解得:0<p≤ ,
,
此时f(x)在x∈(0,3)存在一个极大值;(11分)
②若f(x)在x∈(0,3)恰好两个极值,即h(x)=0在x∈(0,3)有两个不等实根
则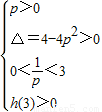 或
或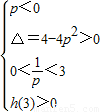 ,解得:
,解得: <p<1,(13分)
<p<1,(13分)
∴0<p<1,
综上所述,当0<p<1时,y=f(x)在x∈(0,3)存在极值.(14分)
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握函数的单调性与导数的关系,掌握函数在某点取得极值的条件,是一道中档题.
(Ⅱ)求出f(x)的导函数,要使函数在定义域内位增函数,即要导函数在定义域内恒大于0,由导函数的分子解出p大于等于一个关系式,利用基本不等式求出这个关系式的最大值,进而得到p的取值范围;
(Ⅲ)求出f(x)的导函数,令导函数等于0得到一个方程,记作(*),设方程的左边为函数h(x),当p=0时求出方程(*)的解为0,显然函数无极值点;当p不为0时,讨论函数有一个极值和两个极值,列出不等式组,求出不等式组的解集即可得到p的取值范围.
解答:解:(I)当p=3时,函数f(x)=3x-
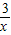 -2lnx,
-2lnx,f(1)=3-3-2ln1=0,f′(x)=3-
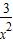 -
-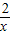 ,
,曲线f(x)在点(1,f(x))处的切线的斜率为f′(1)=3-3-2=4,
∴f(x)在点(1,f(x))处得切线方程为y-0=4(x-1),即y=4x-4;
(Ⅱ)f′(x)=p+
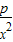 -
-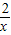 =
=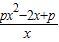 ,(4分)
,(4分)要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0在(0,+∞)内恒成立,
即px2-2x+p≥0在(0,+∞)上恒成立,(5分)
即p≥
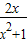 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,设M(x)=
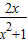 ,(x>0)(6分)
,(x>0)(6分)则M(x)=
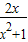 =
=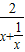 ,
,∵x>0,∴x+
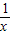 ≥2,当且仅当x=1时取等号,(7分)
≥2,当且仅当x=1时取等号,(7分)∴M(x)≤1,即M(x)max=1,∴p≥1,
所以实数p的取值范围是[1,+∞);(8分)
(Ⅲ)∵f′(x)=
 ,令f′(x)=0,即px2-2x+p=0(*)(9分)
,令f′(x)=0,即px2-2x+p=0(*)(9分)设h(x)=px2-2x+p,x∈(0,3),
当p=0时,方程(*)的解为x=0,此时f(x)在x∈(0,3)无极值,所以p≠0;
当p≠0时,h(x)=px2-2x+p的对称轴方程为x=
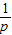 ,
,①若f(x)在x∈(0,3)恰好有一个极值,
则
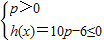 或
或 ,解得:0<p≤
,解得:0<p≤ ,
,此时f(x)在x∈(0,3)存在一个极大值;(11分)
②若f(x)在x∈(0,3)恰好两个极值,即h(x)=0在x∈(0,3)有两个不等实根
则
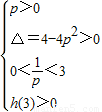 或
或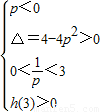 ,解得:
,解得: <p<1,(13分)
<p<1,(13分)∴0<p<1,
综上所述,当0<p<1时,y=f(x)在x∈(0,3)存在极值.(14分)
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握函数的单调性与导数的关系,掌握函数在某点取得极值的条件,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目