题目内容
如右图,扇形OAB的半径为1,中心角60°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.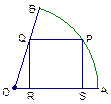

点P为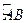 的中点,P(
的中点,P(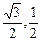 ),最大面积是
),最大面积是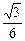
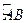 的中点,P(
的中点,P(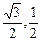 ),最大面积是
),最大面积是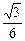
以OA为x轴 O为原点,建立平面直角坐标系,
O为原点,建立平面直角坐标系,
并设P的坐标为(cosθ,sinθ),则
|PS|=sinθ 直线OB的方程为y=
直线OB的方程为y=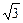 x,直线PQ的方程为y=sinθ
x,直线PQ的方程为y=sinθ 联立解之得Q(
联立解之得Q(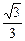 sinθ;sinθ),所以|PQ|=cosθ-
sinθ;sinθ),所以|PQ|=cosθ-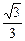 sinθ
sinθ
于是SPQRS=sinθ(cosθ-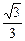 sinθ)
sinθ)
=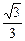 (
(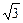 sinθcosθ-sin2θ)=
sinθcosθ-sin2θ)=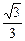 (
(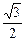 sin2θ-
sin2θ-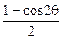 )
)
=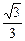 (
(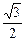 sin2θ+
sin2θ+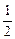 cos2θ-
cos2θ-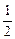 )=
)=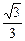 sin(2θ+
sin(2θ+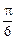 )-
)-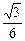

∵0<θ<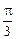 ,∴
,∴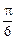 <2θ+
<2θ+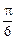 <
<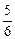 π
π ∴
∴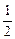 <sin(2θ+
<sin(2θ+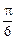 )≤1
)≤1
∴sin(2θ+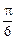 )=1时,PQRS面积最大,且最大面积是
)=1时,PQRS面积最大,且最大面积是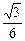 ,
,
此时,θ=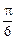 ,点P为
,点P为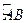 的中点,P(
的中点,P(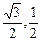 ).
).
 O为原点,建立平面直角坐标系,
O为原点,建立平面直角坐标系,并设P的坐标为(cosθ,sinθ),则
|PS|=sinθ
 直线OB的方程为y=
直线OB的方程为y=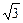 x,直线PQ的方程为y=sinθ
x,直线PQ的方程为y=sinθ 联立解之得Q(
联立解之得Q(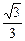 sinθ;sinθ),所以|PQ|=cosθ-
sinθ;sinθ),所以|PQ|=cosθ-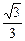 sinθ
sinθ
于是SPQRS=sinθ(cosθ-
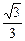 sinθ)
sinθ)=
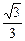 (
(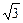 sinθcosθ-sin2θ)=
sinθcosθ-sin2θ)=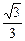 (
(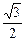 sin2θ-
sin2θ-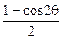 )
)=
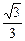 (
(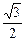 sin2θ+
sin2θ+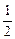 cos2θ-
cos2θ-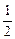 )=
)=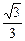 sin(2θ+
sin(2θ+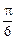 )-
)-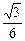

∵0<θ<
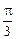 ,∴
,∴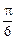 <2θ+
<2θ+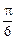 <
<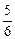 π
π ∴
∴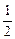 <sin(2θ+
<sin(2θ+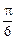 )≤1
)≤1
∴sin(2θ+
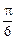 )=1时,PQRS面积最大,且最大面积是
)=1时,PQRS面积最大,且最大面积是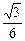 ,
,此时,θ=
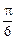 ,点P为
,点P为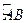 的中点,P(
的中点,P(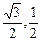 ).
).
练习册系列答案
相关题目
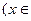 R
R .
.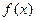 的最小正周期;
的最小正周期;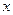 的值.
的值.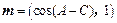 和
和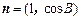 满足
满足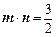 .
.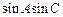 的值;
的值;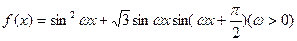
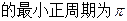 (1)求
(1)求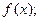
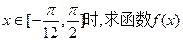 的值域。
的值域。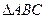 中,角
中,角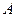 、
、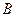 、
、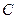 的对边分别为
的对边分别为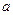 、
、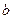 、
、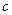 ,且
,且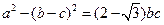 ,
,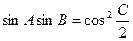 ,
,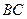 边上中线
边上中线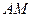 的长为
的长为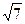 .
. 。
。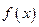 的最小正周期,并判断奇偶性;
的最小正周期,并判断奇偶性;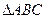 的三个内角,若
的三个内角,若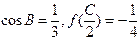 ,且C为锐角,求
,且C为锐角,求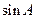 。
。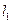 、
、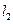 、
、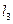 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.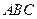 的三顶点分别放在
的三顶点分别放在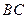 和
和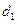 ,
,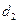 ,求
,求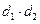 的范围?
的范围?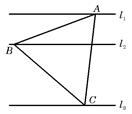
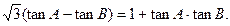
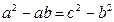 ,求A、B、C的大小;
,求A、B、C的大小;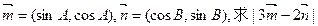 的取值范围.
的取值范围.