题目内容
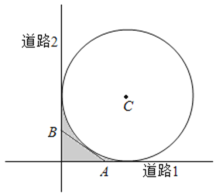
【题目】如图，某城市有一块半径为
（单位：百米）的圆形景观，圆心为
，有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处
图中阴影部分
只有一块绿化地，后来有众多市民建议在绿化地上建一条小路，便于市民快捷地往返两条道路.规划部门采纳了此建议，决定在绿化地中增建一条与圆相切的小道
问：
两点应选在何处可使得小道
最短？
【答案】当
两点离道路的交点都为
（百米）时，小道
最短
【解析】
分别由两条道路所在直线建立直角坐标系
，设
，
，求得直线的方程和圆的方程，运用直线和圆相切的条件：
，求得
的关系，再由两点的距离公式和基本不等式，解不等式可得的最小值，以及此时的位置.
解：如图，分别由两条道路所在直线建立直角坐标系xOy.
设，，
则直线方程为
，即
.
因为与圆
相切，所以
化简得
，即
因此
因为
，
，所以
于是
又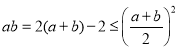
解得
，或
因为，所以
所以
当且仅当
时取等号
所以最小值为
，此时
答：当两点离道路的交点都为（百米）时，小道最短
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
