题目内容
已知M (-2,0), N (2,0), 则以MN为斜边的直角三角形直角顶点P的轨迹方程是( )
A. |
B. |
C. |
D. |
D
解析试题分析:设P(x,y),则由两点间距离公式、勾股定理得x2+4x+4+y2+x2-4x+4+y2=16,x≠±2,
整理,得x2+y2=4(x≠±2).
故选D.
考点:求轨迹方程
点评:简单题,求点的轨迹方程,方法较为灵活。本题利用“直接法”,充分利用点满足的几何条件,得到轨迹方程。

练习册系列答案
相关题目
若直线 与曲线
与曲线 有交点,则( )
有交点,则( )
A. 有最大值 有最大值 ,最小值 ,最小值 | B. 有最大值 有最大值 ,最小值 ,最小值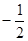 |
C. 有最大值0,最小值 有最大值0,最小值  | D. 有最大值0,最小值 有最大值0,最小值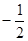 |
点 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
圆 的圆心坐标和半径分别为
的圆心坐标和半径分别为
A. | B. | C. | D. |
M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.相切或相交 |
直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相离 | B.相交 | C.相切 | D.不确定 |
直线 与圆
与圆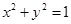 交于不同两点
交于不同两点 、
、 ,
, 为坐标原点,则“
为坐标原点,则“ ”是“向量
”是“向量 、
、 满足
满足 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
当曲线y= 与直线kx-y-2k+3=0有两个相异的交点时,实数k的取值范围是 ( )
与直线kx-y-2k+3=0有两个相异的交点时,实数k的取值范围是 ( )
A.(0, ) ) | B.( , , ] ] | C.( , , ] ] | D.( ,+∞) ,+∞) |
 与圆
与圆 交于不同的两点
交于不同的两点 若
若 ,
, 是坐标原点,那么实数
是坐标原点,那么实数 的取值范围是( )
的取值范围是( )


