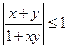题目内容
在平面几何里,有“若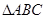 的三边长分别为
的三边长分别为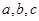 ,其内切圆半径为
,其内切圆半径为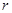 ,则三角形面积为
,则三角形面积为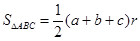 ”. 类比上述结论,拓展到空间,我们有 “若四面体
”. 类比上述结论,拓展到空间,我们有 “若四面体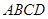 的四个面的面积分别为
的四个面的面积分别为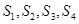 ,其内切球的半径为
,其内切球的半径为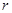 ,则四面体的体积为 ”.
,则四面体的体积为 ”.
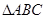 的三边长分别为
的三边长分别为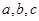 ,其内切圆半径为
,其内切圆半径为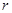 ,则三角形面积为
,则三角形面积为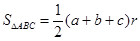 ”. 类比上述结论,拓展到空间,我们有 “若四面体
”. 类比上述结论,拓展到空间,我们有 “若四面体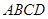 的四个面的面积分别为
的四个面的面积分别为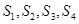 ,其内切球的半径为
,其内切球的半径为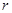 ,则四面体的体积为 ”.
,则四面体的体积为 ”.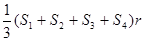
解:利用三角形的分割法,利用内切圆的半径为同一的高,求解面积的思想,类推到空间,将四面体分为四个三棱锥,高都为内切球的半径,这样可以得到结论。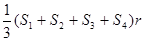
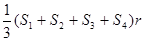

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
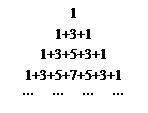
 是自然数,所以
是自然数,所以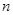 行
行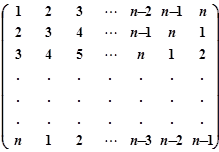
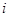 行第
行第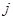 列的数为
列的数为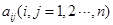 。
。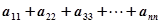 = ▲ ;(2分)
= ▲ ;(2分)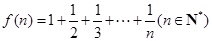 ,计算得
,计算得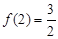 ,
,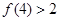 ,
,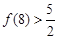 ,
,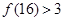 ,
,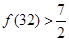 .由此推测,当
.由此推测,当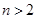 时,有 .
时,有 .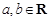 ,若
,若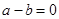 ,则
,则 ,类比得已知
,类比得已知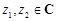 ,若
,若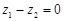 ,则
,则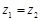 ;
;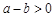 ,则
,则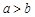 类比得已知
类比得已知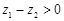 ,则
,则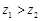 ;
; 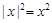 类比得复数
类比得复数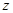 的性质
的性质 ;
; ,若复数
,若复数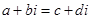 ,则
,则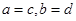 ,类比得已知
,类比得已知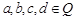 ,若
,若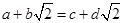 ,则
,则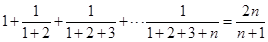 时,由n=k到n=k+1左边需要添加的项是 ___________
时,由n=k到n=k+1左边需要添加的项是 ___________ 满足
满足 ,
, 求证:
求证: