题目内容
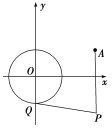
【题目】如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F. 
(1)证明:EC=EF;
(2)如果DC= ![]() BD=3,试求DE的长.
BD=3,试求DE的长.
【答案】
(1)证明:由圆内接四边形的性质,可求得∠ABC=∠CDE;
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠ADB=∠EDF,
∴∠CDE=∠EDF,
∵BD是圆的直径,
∴BC⊥DC,
∵EF⊥BD,DE=DE,
∴△DEF≌△DEC,
∴EC=EF
(2)解:∵DC= ![]() BD=3,BC⊥DC,
BD=3,BC⊥DC,
∴∠BDC=60°,
∴∠BAC=60°,
∴∠ABC=60°,
∴∠EDC=60°,
∴∠BDC=∠EDC,
∵DC⊥BC,
∴DE=BD=6.
【解析】(1)通过证明△DEF≌△DEC,即可证明:EC=EF;(2)如果DC= ![]() BD=3,证明∠BDC=∠EDC,利用等腰三角形的性质求DE的长.
BD=3,证明∠BDC=∠EDC,利用等腰三角形的性质求DE的长.

练习册系列答案
相关题目