题目内容
(12分) 已知数列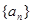 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: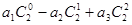 ,
,
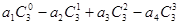
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
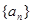 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.(1)求和:
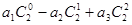 ,
,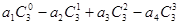
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(1)
(2)归纳概括的结论为:若数列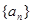 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则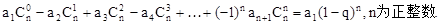
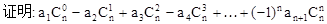

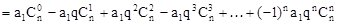
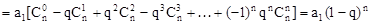
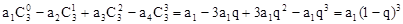 |
(2)归纳概括的结论为:若数列
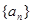 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则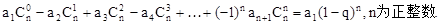
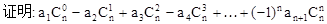

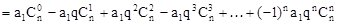
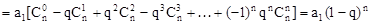
本试题主要是考查了归纳猜想的思想的运用,根据已知的前即项得到后面的关系式。
(1)因为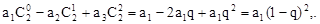
(2)归纳概括的结论为:若数列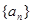 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则
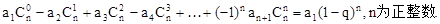 ,然后证明。
,然后证明。
(1)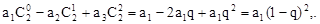 ………………3分
………………3分
………6分
(2)归纳概括的结论为:若数列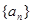 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则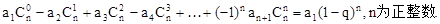
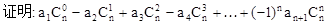

………………………9分
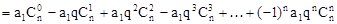 ………………………………11分
………………………………11分
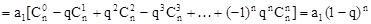 ……………………12分
……………………12分
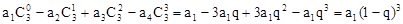 |
(1)因为
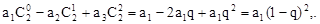
(2)归纳概括的结论为:若数列
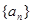 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则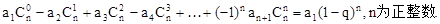 ,然后证明。
,然后证明。(1)
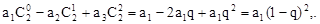 ………………3分
………………3分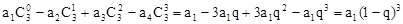 |
………6分
(2)归纳概括的结论为:若数列
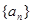 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则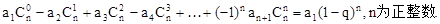
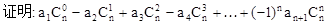

………………………9分
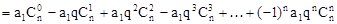 ………………………………11分
………………………………11分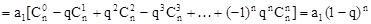 ……………………12分
……………………12分
练习册系列答案
相关题目
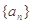 是等比数列,且公比
是等比数列,且公比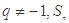 是
是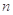 项和,已知
项和,已知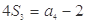 ,
,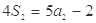 ,则公比
,则公比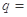 ( )
( )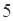



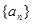 是公比为
是公比为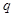 的等比数列,首项
的等比数列,首项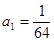 ,
,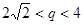 ,对于
,对于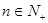 ,
,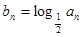 ,若数列
,若数列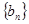 的前
的前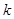 项和取得最大值,则
项和取得最大值,则 的前n项和为
的前n项和为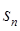 ,且4
,且4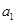 ,2
,2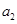 ,
,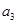 成等差数列。若
成等差数列。若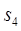 =( )
=( ) 中,
中, ,
, ,(
,( ),则通项公式
),则通项公式 。
。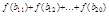 =
= 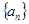 中,
中,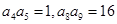 ,则
,则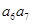 等于
等于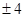
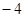
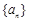 中,
中,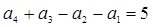 ,则
,则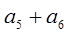 的最小值是________
的最小值是________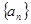 中,若
中,若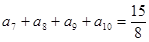 ,
,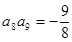 ,则
,则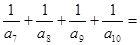 ____________
____________