题目内容
在△ABC中,已知tanB=
.
(1)试判断△ABC的形状,并给出证明;
(2)若∠C=60°,AB=1,求△ABC的面积.
| cos(C-B) | sinA+sin(C-B) |
(1)试判断△ABC的形状,并给出证明;
(2)若∠C=60°,AB=1,求△ABC的面积.
分析:(1)通过切化弦,由
=
可求得cos(C+B)=-cosA=0,从而可判断△ABC的形状;
(2)依题意,可求得AC=
,利用三角形的面积公式即可求得答案.
| sinB |
| cosB |
| cos(C-B) |
| sinA+sin(C-B) |
(2)依题意,可求得AC=
| ||
| 3 |
解答:解:(1)由题意得,
=
=
=tanB=
,
所以cosCcosB+sinCsinB=2sinCsinB,
即有cosCcosB-sinCsinB=0,
即cos(C+B)=-cosA=0,
所以∠A=90°,即△ABC是直角三角形.
(2)因为∠C=60°,AB=1,
又由(1)得:AC=ABtan30°=
,
所以△ABC的面积为
×AC×AB=
.
| cos(C-B) |
| sinA+sin(C-B) |
=
| cos(C-B) |
| sin(C+B)+sin(C-B) |
=
| cosCcosB+sinCsinB |
| 2sinCcosB |
=tanB=
| sinB |
| cosB |
所以cosCcosB+sinCsinB=2sinCsinB,
即有cosCcosB-sinCsinB=0,
即cos(C+B)=-cosA=0,
所以∠A=90°,即△ABC是直角三角形.
(2)因为∠C=60°,AB=1,
又由(1)得:AC=ABtan30°=
| ||
| 3 |
所以△ABC的面积为
| 1 |
| 2 |
| ||
| 6 |
点评:本题考查三角形的形状判断,考查三角函数中的恒等变换应用,考查分析与运算能力,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.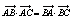 .
. |=|
|=| |;
|; ,求|
,求| -t
-t