题目内容
在△ABC中,已知B(-3,0),C(3,0),D为线段BC上一点, ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
.(Ⅰ)求点H的轨迹M的方程;
(Ⅱ)若过C点且斜率为
 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
【答案】分析:(Ⅰ)设H(x,y),A(x,y),则由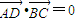 知,AD是△ABC的高,所以x=x.由
知,AD是△ABC的高,所以x=x.由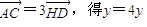 .由此能求出点H的轨迹M的方程.
.由此能求出点H的轨迹M的方程.
(Ⅱ)役直线CP的方程为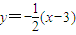 .由
.由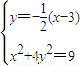 ,解得点P的坐标为
,解得点P的坐标为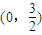 .由此进行分类讨论,能求出当△CPQ为锐角三角形时t的取值范围.
.由此进行分类讨论,能求出当△CPQ为锐角三角形时t的取值范围.
解答:解:(Ⅰ)设H(x,y),A(x,y),
则由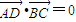 知,AD是△ABC的高,
知,AD是△ABC的高,
∴x=x.
由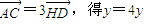 .
.
∴A(x,4y).…(1分)
∴ .…(2分)
.…(2分)
∵H是△ABC的垂心,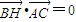 ,…(4分)
,…(4分)
∴(3-x,-4y)•(x+3,y)=0,
即x2+4y2=9(y≠0).…(6分)(y≠0漏写扣1分)
(Ⅱ)直线CP的方程为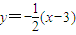 .
.
由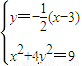 ,
,
解得点P的坐标为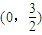 .…(7分)
.…(7分)
(i)∵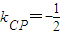 ,
,
∴当∠PCQ是锐角时,点Q只能在点C的左侧,此时t<3.…(8分)
(ii)当∠PQC为锐角时,kPQ>0,此时t<0;…(9分)
(iii)当∠QPC为锐角时,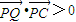 ,
,
即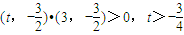 .…(11分)
.…(11分)
∴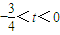 .…(12分)
.…(12分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点,易错点是知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
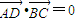 知,AD是△ABC的高,所以x=x.由
知,AD是△ABC的高,所以x=x.由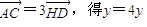 .由此能求出点H的轨迹M的方程.
.由此能求出点H的轨迹M的方程.(Ⅱ)役直线CP的方程为
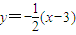 .由
.由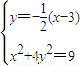 ,解得点P的坐标为
,解得点P的坐标为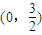 .由此进行分类讨论,能求出当△CPQ为锐角三角形时t的取值范围.
.由此进行分类讨论,能求出当△CPQ为锐角三角形时t的取值范围.解答:解:(Ⅰ)设H(x,y),A(x,y),
则由
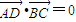 知,AD是△ABC的高,
知,AD是△ABC的高,∴x=x.
由
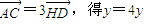 .
.∴A(x,4y).…(1分)
∴
 .…(2分)
.…(2分)∵H是△ABC的垂心,
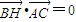 ,…(4分)
,…(4分)∴(3-x,-4y)•(x+3,y)=0,
即x2+4y2=9(y≠0).…(6分)(y≠0漏写扣1分)
(Ⅱ)直线CP的方程为
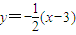 .
.由
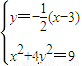 ,
,解得点P的坐标为
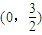 .…(7分)
.…(7分)(i)∵
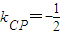 ,
,∴当∠PCQ是锐角时,点Q只能在点C的左侧,此时t<3.…(8分)
(ii)当∠PQC为锐角时,kPQ>0,此时t<0;…(9分)
(iii)当∠QPC为锐角时,
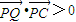 ,
,即
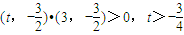 .…(11分)
.…(11分)∴
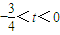 .…(12分)
.…(12分)点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点,易错点是知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 在△ABC中,已知B=45°,D是BC上一点,AD=5,AC=7,DC=3,求AB的长.
在△ABC中,已知B=45°,D是BC上一点,AD=5,AC=7,DC=3,求AB的长. 如图,在△ABC中,已知B=
如图,在△ABC中,已知B=