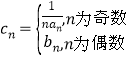题目内容
【题目】选修4-4：坐标系与参数方程
在直角坐标系 
中，直线 
的参数方程为 
（ 
为参数），以原点为极点， 
轴正半轴为极轴建立极坐标系，圆 
的极坐标方程为 
.
（1）写出直线 的普通方程及圆 的直角坐标方程；
（2）点 
是直线 上的点，求点 的坐标，使 到圆心 的距离最小.
【答案】
（1）解：由 
消去参数 
，得直线 
的普通方程为 
，
由 
得 
， 
，即圆 
的直角坐标方程为 
（2）解： 
， 
， 
，
时 
最小，此时 
.
【解析】(1)根据题意结合已知条件消参化为直线的一般方程，再由参数方程与直角坐标方程的互化关系即可得出圆的直角坐标方程。(2)根据题意把点的坐标代入到两点间的结论公式整理可得出关于t的一元二次方程，借助二次函数的最值求出点P到圆心的最小距离。
【考点精析】认真审题，首先需要了解直线的参数方程(经过点
，倾斜角为
的直线
的参数方程可表示为
（
为参数）)．
练习册系列答案
相关题目
【题目】某学校高三年级有学生1 000名，经调查，其中750名同学经常参加体育锻炼(称为A类同学)，另外250名同学不经常参加体育锻炼(称为B类同学)，现用分层抽样方法(按A类、B类分两层)从该年级的学生中共抽查100名同学，如果以身高达165 cm作为达标的标准，对抽取的100名学生，得到以下列联表：
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
（1）完成上表；
（2）能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(K2的观测值精确到0.001)?
