题目内容
【题目】定义在R上的函数f（x）满足f（x+2）= 
f（x），当x∈[0，2]时，f（x）= 
，函数g（x）=x3+3x2+m．若对任意s∈[﹣4，﹣2），存在t∈[﹣4，﹣2），不等式f（s）﹣g（t）≥0成立，则实数m的取值范围是（ ）
A.（﹣∞，﹣12]
B.（﹣∞，14]
C.（﹣∞，﹣8]
D.（﹣∞， 
]
【答案】B
【解析】解：对任意s∈[﹣4，﹣2），存在t∈[﹣4，﹣2），不等式f（s）﹣g（t）≥0成立， 等价于：f（s）min≥g（t）min ．
定义在R上的函数f（x）满足f（x+2）= 
f（x），当x∈[0，2]时，f（x）=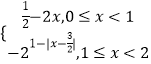 
，
令x∈[﹣4，﹣2），则（x+4）∈[0，2]，f（x）= 
，
﹣4≤x＜﹣3时，f（x）=﹣2x﹣ 
＞﹣2×（﹣3）﹣ =﹣ 
．
﹣3≤x＜﹣2时，f（x）=﹣ 
≥﹣2．
可得f（x）min=﹣2．
函数g（x）=x3+3x2+m，x∈[﹣4，﹣2），
g′（x）=3x2+6x=3x（x+2）＞0，∴函数g（x）在x∈[﹣4，﹣2）单调递增，
∴g（x）min=g（﹣4）=﹣64+48+m=m﹣16，
由题意可得：﹣2≥m﹣16，解得m≤14．
∴实数m的取值范围是（﹣∞，14]
故选：B．
练习册系列答案
相关题目
【题目】某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：
周销售量 | 2 | 3 | 4 |
频数 | 20 | 50 | 30 |
（1）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；
（2）已知每吨该商品的销售利润为2千元，ξ表示该种商品两周销售利润的和（单位：千元），若以上述频率作为概率，且各周的销售量相互独立，求ξ的分布列和数学期望．
