题目内容
在△ABC中,BC=a,AC=b,且a,b是方程x2-2
x+2=0的两根,又2cos(A+B)=1,
(1)求角C的度数;
(2)求AB的长;
(3)△ABC的面积.
| 3 |
(1)求角C的度数;
(2)求AB的长;
(3)△ABC的面积.
(1)△ABC中,∵cosC=-cos(A+B)=-
,∴C=120°.
(2)根据一元二次方程根与系数的关系可得 a+b=2
,ab=2,
由余弦定理可得 AB=
=
=
.
(3)△ABC的面积等于
absinC=sin120°=
.
| 1 |
| 2 |
(2)根据一元二次方程根与系数的关系可得 a+b=2
| 3 |
由余弦定理可得 AB=
| a2+b2-2abcosC |
| (a+b)2-ab |
| 10 |
(3)△ABC的面积等于
| 1 |
| 2 |
| ||
| 2 |

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 ,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.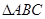 的内角A,B,C所对的边分别为a,b,c,若
的内角A,B,C所对的边分别为a,b,c,若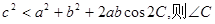 的可能取值为( ).
的可能取值为( ).
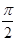
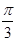
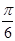
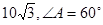 ,则
,则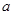 为 ( )
为 ( )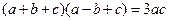 ,
,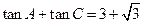 ,
,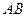 边上的高为
边上的高为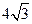 ,求角
,求角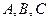 的大小与边
的大小与边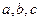 的长
的长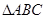 中,
中,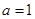 ,
,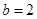 ,
,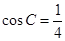 ,则
,则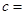 ;
;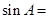 .
.