Question

【题目】（本小题满分14分）如图，在三棱锥P- ABC中，已知平面PBC平面ABC．

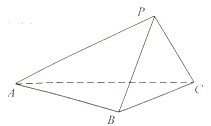
（1）若ABBC，CPPB，求证：CPPA：

（2）若过点A作直线⊥平面ABC，求证： //平面PBC．

Answer 1

【答案】（1）详见解析，（2）详见解析

【解析】【试题分析】（1）依据题设借助面面垂直的性质定理证明平面平面，然后运用线面垂直的性质定理证明；（2）借助题设条件先证明平面，进而确定，然后再运用线面平行的性质定理推证：

证明：（1）因为平面 平面 ，平面 平面， 平面， ，所以平面.因为平面，所以 .又因为 平面所以平面又因为平面所以.

(2)在平面内过点作垂足为因为平面平面，

又平面平面 平面，所以平面又平面，所以又平面 平面，所以平面.