Question

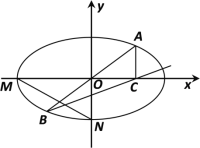
【题目】在平面直角坐标系中，椭圆的上顶点为A，左、右焦点分别为，，直线的斜率为，点在椭圆E上，其中P是椭圆上一动点，Q点坐标为.

(1)求椭圆E的标准方程；

(2)作直线l与x轴垂直，交椭圆于两点（两点均不与P点重合)，直线，与x轴分别交于点.求的最小值及取得最小值时点P的坐标.

Answer 1

【答案】（1）（2）的最小值为，此时点P的坐标为或

【解析】

（1）根据直线的斜率求得，将点坐标代入托运方程，解出的值，进而求得的值以及椭圆方程.（2）设出三个点的坐标，由直线的方程求得点坐标以及,由直线的方程求得点坐标以及.利用基本不等式求得的最小值.根据基本不等式等号成立的条件以及绝对值的性质，求出点的坐标.

(1)由直线的斜率为可知直线的倾斜角为.

在中，,于是,

椭圆,将代入得

所以，椭圆E的标准方程

(2)设点.

于是，直线,令,

所以

直线，令，

所以

又.代入上式并化简

即，

当(即)时取得最小值，

（Ⅰ）时，化简得

根据题意：，若亦与题意不符，

所以，此时或

（Ⅱ）时，化简得

将代入并化简得：

根据题意：，若，而

所以 不成立，即不成立

综上，或，点P的坐标为或