题目内容
1.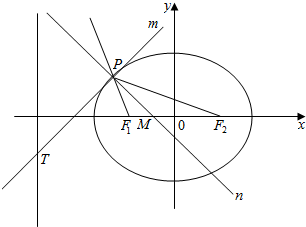 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,定点A(-$\frac{1}{2}$,$\frac{3\sqrt{5}}{4}$)在椭圆上,F1,F2为椭圆的左、右焦点,定直线l的方程为x=-4,过椭圆上一点P作切线m与l交于T点,过P且垂直于直线m的直线n交F1F2于点M.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,定点A(-$\frac{1}{2}$,$\frac{3\sqrt{5}}{4}$)在椭圆上,F1,F2为椭圆的左、右焦点,定直线l的方程为x=-4,过椭圆上一点P作切线m与l交于T点,过P且垂直于直线m的直线n交F1F2于点M.(1)求椭圆的方程;
(2)设椭圆的离心率为e,求证:$\frac{{F}_{1}M}{P{F}_{1}}$=e;
(3)证明PM为∠F1PF2的平分线.
分析 (1)利用离心率找到a,b,c的关系,把方程中的a,b用c表示,代入定点坐标;(2)设点P的坐标,求出M点的坐标,把PF1,F1M用点P的坐标表示(3)用(2)中求得的坐标,结合内角平分线定理进行证明,用焦半径计算公式求PF1 和PF2
解答 解:(1)设椭圆的半焦距为c,
因为e=$\frac{1}{2}$,所以$\frac{c}{a}=\frac{1}{2}$,a2=4c2,b2=3c2,则椭圆的方程变为
$\frac{{x}^{2}}{4{c}^{2}}+\frac{{y}^{2}}{3{c}^{2}}=1$
代入点A(-$\frac{1}{2}$,$\frac{3\sqrt{5}}{4}$)的坐标得到:c2=1
故椭圆的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
(2)设P(x0,y0),
因为椭圆的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,所以$\frac{2x}{4}+\frac{2y{y}^{'}}{3}=0$,即$y'=-\frac{3x}{4y}$,所以直线n的斜率是$\frac{4{y}_{0}}{3{x}_{0}}$
∴直线n的方程是:$y-{y}_{0}=\frac{4{y}_{0}}{3{x}_{0}}(x-{x}_{0})$,
在直线方程中令y=0,得到${x}_{M}=\frac{{x}_{0}}{4}$
因为
$\frac{{F}_{1}M}{P{F}_{1}}=\frac{\frac{{x}_{0}}{4}-(-1)}{2+\frac{1}{2}{x}_{0}}=\frac{{x}_{0}+4}{8+2{x}_{0}}=\frac{1}{2}=e$
所以结论成立
(3)由(2)知点M($\frac{{x}_{0}}{4},0$)
因为
$\frac{P{F}_{1}}{P{F}_{2}}=\frac{a+e{x}_{0}}{a-e{x}_{0}}=\frac{2+\frac{1}{2}{x}_{0}}{2-\frac{1}{2}{x}_{0}}=\frac{4+{x}_{0}}{4-{x}_{0}}$,$\frac{{F}_{1}M}{M{F}_{2}}=\frac{\frac{{x}_{0}}{4}+1}{1-\frac{{x}_{0}}{4}}=\frac{4+{x}_{0}}{4-{x}_{0}}$
所以
$\frac{P{F}_{1}}{P{F}_{2}}=\frac{{F}_{1}M}{M{F}_{2}}$
即PM是∠F1PF2的角平分线
所以结论成立
点评 (1)利用方程思想解出椭圆的方程;(2)求直线m的斜率用的复合函数的求导,也可以用判别式法,但是求导比判别式简单;(3)第(2)解出点M的坐标后,本小题就比较简单了,但是要用到内角平分线定理.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案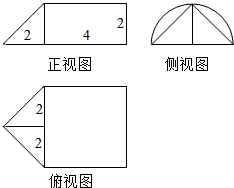
| A. | $\frac{1}{3}$+π | B. | $\frac{2}{3}$+2π | C. | $\frac{8}{3}$+8π | D. | $\frac{4}{3}$+4π |
| A. | 1:8 | B. | 1:10 | C. | $\sqrt{10}$:10 | D. | $\sqrt{5}$:5 |