题目内容
9.已知函数f(x)的定义域为R且f(x)=$\left\{\begin{array}{l}{{x}^{2}+2,x∈[0,1]}\\{2-{x}^{2},x∈(-1,0)}\end{array}\right.$,f(x+1)=f(x-1),则方程f(x)=$\frac{2x+1}{x}$在区间[-3,3]的所有实根之和为( )| A. | -8 | B. | -2 | C. | 0 | D. | 1 |
分析 由题意作出函数y=f(x)与函数y=$\frac{2x+1}{x}$在区间[-3,3]上的图象,结合图象求解即可.
解答 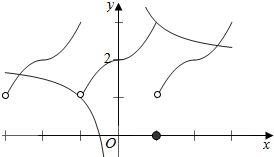 解:∵f(x+1)=f(x-1),即有f(x+2)=f(x),
解:∵f(x+1)=f(x-1),即有f(x+2)=f(x),
∴f(x)是周期为2的周期函数,
又∵f(x)=$\left\{\begin{array}{l}{{x}^{2}+2,x∈[0,1]}\\{2-{x}^{2},x∈(-1,0)}\end{array}\right.$,
作函数f(x)与函数y=2+$\frac{1}{x}$在区间[-3,3]上
的图象如右:
结合图象可知,
图象共有3个交点,即共有3个实根,其中有两个关于原点对称,第三个为1;
故其实根之和为1;
故选D.
点评 本题考查了分段函数与周期函数的图象及性质,同时考查了方程的根与函数的图象的交点的关系应用及数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
19.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的两个焦点为F1,F2,过F1作垂直于x轴的直线与椭圆相交,其中一个交点为P,则|PF2|的值为( )
| A. | $\frac{47}{5}$ | B. | $\frac{34}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{16}{5}$ |
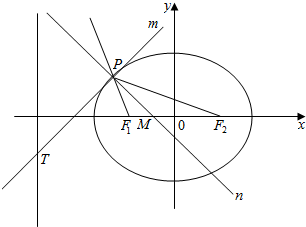 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,定点A(-$\frac{1}{2}$,$\frac{3\sqrt{5}}{4}$)在椭圆上,F1,F2为椭圆的左、右焦点,定直线l的方程为x=-4,过椭圆上一点P作切线m与l交于T点,过P且垂直于直线m的直线n交F1F2于点M.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,定点A(-$\frac{1}{2}$,$\frac{3\sqrt{5}}{4}$)在椭圆上,F1,F2为椭圆的左、右焦点,定直线l的方程为x=-4,过椭圆上一点P作切线m与l交于T点,过P且垂直于直线m的直线n交F1F2于点M.