题目内容
已知函数f(x)=sinxcosx-
sin(2x-
).
(1)求f(
)的值;
(2)求f(x)的最小正周期及单调区间;
(3)求f(x)在[0,
]上的最大值与最小值及相应的x的值.
| 1 |
| 2 |
| π |
| 3 |
(1)求f(
| 4π |
| 3 |
(2)求f(x)的最小正周期及单调区间;
(3)求f(x)在[0,
| π |
| 2 |
考点:两角和与差的正弦函数,三角函数的周期性及其求法,三角函数的最值
专题:三角函数的求值,三角函数的图像与性质
分析:(1)化简可得f(x)=
sin(2x+
),从而可求得f(
)的值.
(2)由周期公式可得T的值,由2kπ-
≤2x+
≤
+2kπ k∈Z,2kπ+
≤2x+
≤
+2kπ k∈Z,即可求出单调区间;
(3)先求出2x+
∈[
,
],从而可求f(x)在[0,
]上的最大值与最小值及相应的x的值.
| 1 |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
(2)由周期公式可得T的值,由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
(3)先求出2x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| π |
| 2 |
解答:
解:(1)∵f(x)=sinxcosx-
sin(2x-
)=
sin2x-
(
sin2x-
cos2x)=
sin(2x+
).
∴f(
)=
sin(2×
+
)=
sin3π=0.
(2)∵f(x)=
sin(2x+
),
∴T=
=π.
由2kπ-
≤2x+
≤
+2kπ k∈Z,即kπ-
≤x≤
+kπ(k∈Z),
所以函数的单调增区间为:[-
+kπ,
+kπ](k∈Z).
由2kπ+
≤2x+
≤
+2kπ(k∈Z),即kπ+
≤x≤
+kπ(k∈Z),
所以函数的单调减区间为:[kπ+
,
+kπ](k∈Z).
(3)∵x∈[0,
],∴2x+
∈[
,
]
∴当x=
时,f(x)max=
×1=
;当x=
时,f(x)min=
sin
=-
.
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴f(
| 4π |
| 3 |
| 1 |
| 2 |
| 4π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
(2)∵f(x)=
| 1 |
| 2 |
| π |
| 3 |
∴T=
| 2π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
所以函数的单调增区间为:[-
| 5π |
| 12 |
| π |
| 12 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
所以函数的单调减区间为:[kπ+
| π |
| 12 |
| 7π |
| 12 |
(3)∵x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴当x=
| π |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| 4π |
| 3 |
| ||
| 4 |
点评:本题主要考察了三角函数的周期性及其求法,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对两条不相交的空间直线a与b,必存在平面α,使得( )
| A、a?α,b?α |
| B、a?α,b∥α |
| C、a⊥α,b⊥α |
| D、a?α,b⊥α |
有四个数a1,a2,a3,a4,前三个数成等比,积为64;后三个数成等差,和为6;则a1=( )
| A、9 | B、8 | C、16 | D、4 |
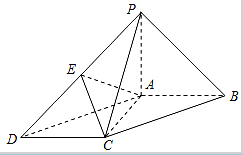 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.