题目内容
已知函数f(x)=2|2x-m|(m为常数),若f(x)在区间[2,+∞)上是增函数,则m的取值范围是________.
(-∞,4]
令t=|2x-m|,则t=|2x-m|在区间[ ,+∞)上单调递增,在区间(-∞,
,+∞)上单调递增,在区间(-∞, ]上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2|2x-m|在[2,+∞)上单调递增,则有
]上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2|2x-m|在[2,+∞)上单调递增,则有 ≤2,即m≤4,所以m的取值范围是(-∞,4].故填(-∞,4].
≤2,即m≤4,所以m的取值范围是(-∞,4].故填(-∞,4].
 ,+∞)上单调递增,在区间(-∞,
,+∞)上单调递增,在区间(-∞, ]上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2|2x-m|在[2,+∞)上单调递增,则有
]上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2|2x-m|在[2,+∞)上单调递增,则有 ≤2,即m≤4,所以m的取值范围是(-∞,4].故填(-∞,4].
≤2,即m≤4,所以m的取值范围是(-∞,4].故填(-∞,4].
练习册系列答案
相关题目
 )x,g(x)=
)x,g(x)= x,记函数h(x)=
x,记函数h(x)= ,则不等式h(x)≥
,则不等式h(x)≥ 的解集为________.
的解集为________.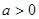 且
且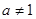 ,则
,则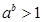 是
是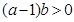 的( )
的( )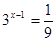 的解是
的解是 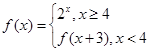 则f(log23)等于 ( )
则f(log23)等于 ( )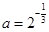 ,
,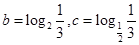 ,则( )
,则( )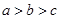
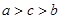
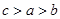
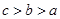
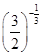 ×
×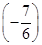 0+
0+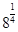 ×
×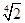 -
- =________.
=________.