题目内容
6.已知α为锐角,cos(α$+\frac{4n+1}{4}$π)=$\frac{1}{2}$,(n∈Z),求cos(α-$\frac{π}{4}$)的值.分析 对n的奇偶性分类,由诱导公式和已知式子可得cos(α+$\frac{π}{4}$),再由同角三角函数基本关系可得sin(α+$\frac{π}{4}$),再由诱导公式可得cos(α-$\frac{π}{4}$)=sin(α+$\frac{π}{4}$),代入可得答案.
解答 解:当n为奇数时,由诱导公式可得cos(α$+\frac{4n+1}{4}$π)=cos(nπ+α+$\frac{π}{4}$)=-cos(α+$\frac{π}{4}$)=$\frac{1}{2}$,
∴cos(α+$\frac{π}{4}$)=-$\frac{1}{2}$,结合α为锐角可得sin(α+$\frac{π}{4}$)=$\sqrt{1-co{s}^{2}(α+\frac{π}{4})}$=$\frac{\sqrt{3}}{2}$,
∴cos(α-$\frac{π}{4}$)=cos[(α+$\frac{π}{4}$)-$\frac{π}{2}$]=cos[$\frac{π}{2}$-(α+$\frac{π}{4}$)]=sin(α+$\frac{π}{4}$)=$\frac{\sqrt{3}}{2}$;
当n为偶数时,由诱导公式可得cos(α$+\frac{4n+1}{4}$π)=cos(nπ+α+$\frac{π}{4}$)=cos(α+$\frac{π}{4}$)=$\frac{1}{2}$,
∴cos(α+$\frac{π}{4}$)=$\frac{1}{2}$,结合α为锐角可得sin(α+$\frac{π}{4}$)=$\sqrt{1-co{s}^{2}(α+\frac{π}{4})}$=$\frac{\sqrt{3}}{2}$,
∴cos(α-$\frac{π}{4}$)=cos[(α+$\frac{π}{4}$)-$\frac{π}{2}$]=cos[$\frac{π}{2}$-(α+$\frac{π}{4}$)]=sin(α+$\frac{π}{4}$)=$\frac{\sqrt{3}}{2}$;
综上可得cos(α-$\frac{π}{4}$)的值为$\frac{\sqrt{3}}{2}$
点评 本题考查三角函数公式,涉及诱导公式和同角三角函数基本关系和分类讨论的思想,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{5}{6}$ | B. | $-\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
| A. | (-∞,-2] | B. | [-2,+∞) | C. | (-∞,-1] | D. | [-1,+∞) |
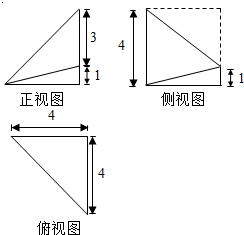 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于$\frac{40}{3}$.