题目内容
10.判断下列各题中的向量$\overrightarrow{a}$与$\overrightarrow{b}$是否共线:(1)$\overrightarrow{a}$=-2$\overrightarrow{e}$,$\overrightarrow{b}$=2$\overrightarrow{e}$
(2)$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=-2$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$.
分析 直接利用向量共线的充要条件判断即可.
解答 解:(1)$\overrightarrow{a}$=-2$\overrightarrow{e}$,$\overrightarrow{b}$=2$\overrightarrow{e}$,可得$\overrightarrow{a}=-\overrightarrow{b}$,向量$\overrightarrow{a}$与$\overrightarrow{b}$共线.
(2)$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=-2$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$.$\overrightarrow{a}=-\frac{1}{2}\overrightarrow{b}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$共线.
点评 本题考查向量共线的充要条件,基本知识的考查.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积为( )
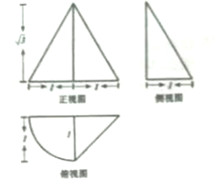

| A. | $\frac{(π+2)\sqrt{3}}{12}$ | B. | $\frac{(π+1)\sqrt{3}}{12}$ | C. | $\frac{(2π+1)\sqrt{3}}{12}$ | D. | $\frac{(2π+3)\sqrt{3}}{12}$ |