题目内容
15．若z=$\frac{（1-2i）^{5}（3+4i）}{（2-i）^{5}}$，则|z|=5．分析 利用复数的运算法则、复数的周期性、模的计算公式即可得出．
解答 解：∵$\frac{1-2i}{2-i}=\frac{（1+2i）（2+i）}{（2-i）（2+i）}$=$\frac{5i}{5}$=i，
∴z=$\frac{（1-2i）^{5}（3+4i）}{（2-i）^{5}}$=i5（3+4i）=i（3+4i）=-4+3i，
∴|z|=$\sqrt{（-4）^{2}+{3}^{2}}$=5．
故答案为：5．
点评 本题考查了复数的运算法则、复数的周期性、模的计算公式，属于基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
铁皮剪出一个圆心角为α的扇形，制成一个圆锥形容器，扇形的圆心角α多大时，容器的容积最大？
3．执行如图所示的程序框图，则输出S的值是（ ）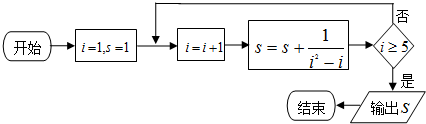
| A． | $\frac{4}{5}$ | B． | $\frac{9}{5}$ | C． | $\frac{5}{6}$ | D． | $\frac{11}{6}$ |