题目内容
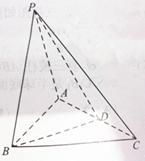
如图,三棱锥P—ABC中,PC⊥平面ABC,PC=AC=2,AB=BC, D是PB上一点,且CD⊥平面PAB.
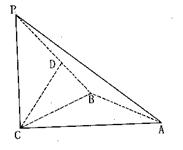
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;

(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
(1)见解析;(2)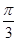 .
.
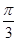 .
. 试题分析:(1)主要考虑证明AB垂直于平面PCB内的两条相交直线.根据PC⊥平面ABC,AB
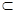 平面ABC,得到PC⊥AB.根据CD⊥平面PAB,AB
平面ABC,得到PC⊥AB.根据CD⊥平面PAB,AB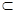 平面PAB,得到OC⊥AB.因此AB平面PCB.
平面PAB,得到OC⊥AB.因此AB平面PCB. (2)有两种思路,
一是“几何法”,通过“一作,二证,三计算”确定异面直线PA与BC所成的角为
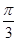 .
. 二是“向量法”,以B为原点,建立如图所示的坐标系.通过确定向量的坐标
利用
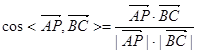

得到异面直线AP与BC所成的角为
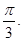
试题解析:解法一:(1)∵PC⊥平面ABC,AB
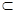 平面ABC,∴PC⊥AB. 2分
平面ABC,∴PC⊥AB. 2分∵CD⊥平面PAB,AB
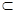 平面PAB,∴OC⊥AB. 3分
平面PAB,∴OC⊥AB. 3分又PC
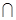 CD=C,∴AB平面PCB. 4分
CD=C,∴AB平面PCB. 4分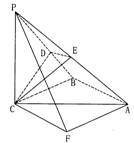
(2)过点A作AF//BC,且AF=BC,连接PF,CF.
则∠PAF为异面直线PA与BC所成的角. 5分
由(1)可得AB⊥BC,∴CF⊥AF.
由三垂线定理,得PF⊥AF。
则AF=CF=
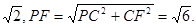
在Rt△PFA中,
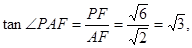
∴异面直线PA与BC所成的角为
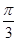 . 12分
. 12分解法二:(1)同解法一.
(2)由(1)AB⊥平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=
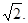
以B为原点,建立如图所示的坐标系.
则A(0,
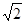 ,0),B(0,0,0),C(
,0),B(0,0,0),C(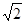 ,0,0),P(
,0,0),P(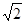 ,0,2).
,0,2).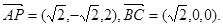 8分
8分则

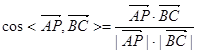

∴异面直线AP与BC所成的角为
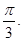 12分
12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
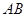 是圆的直径,
是圆的直径,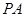 垂直圆所在的平面,
垂直圆所在的平面,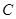 是圆上任一点,
是圆上任一点,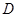 是线段
是线段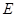 是线段
是线段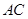 上的一点.
上的一点.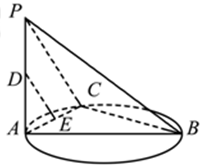
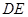 ∥平面
∥平面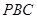 ;
;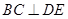 .
.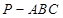 中,
中,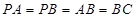 ,
,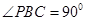 ,D为AC的中点,
,D为AC的中点,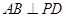 .
.
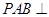 平面
平面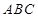 ;
;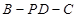 的余弦值.
的余弦值.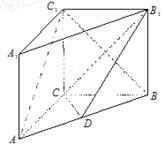
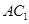 ∥平面
∥平面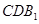 ;
;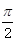 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .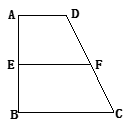
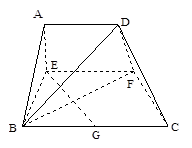
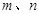 是两条不同的直线,
是两条不同的直线,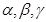 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: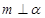 ,
,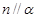 ,则
,则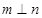
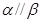 ,
,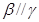 ,
,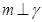
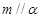 ,
,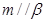 ,
,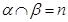 ,则
,则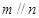
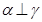 ,
,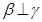 ,
,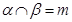 ,则
,则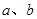 和平面
和平面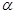 ,下列推论中错误的是( )
,下列推论中错误的是( )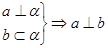
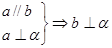
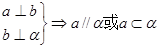
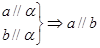
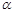 ,
,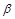 ,
,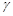 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题: 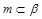 ,
, ,则
,则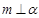 ;
;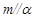 ,
,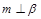 ,则
,则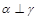 ,则
,则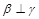 ;
;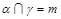 ,
,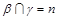 ,
,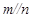 ,则
,则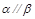 .
.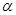 和
和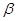 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: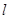 与
与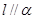 ;
;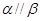 ;
;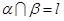 ,若
,若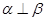 ;
;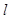 与平面
与平面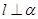 .
.