题目内容
若非零向量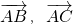 和
和 满足
满足 ,且
,且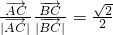 ,则△ABC为
,则△ABC为
- A.等边三角形
- B.等腰非直角三角形
- C.非等腰三角形
- D.等腰直角三角形
D
分析:根据任意一向量与该向量的模的比值都是单位向量,可得: ,进而得到
,进而得到 在∠BAC的角平分线上(设角平分线为AD),再根据两向量的数量积为0,可得两向量垂直可得AD与BC垂直,根据三角形的全等,可得AB=AC,即三角形为等腰三角形,同时由
在∠BAC的角平分线上(设角平分线为AD),再根据两向量的数量积为0,可得两向量垂直可得AD与BC垂直,根据三角形的全等,可得AB=AC,即三角形为等腰三角形,同时由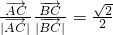 及
及 ,根据平面向量的数量积运算法则可求出C的度数,进而判断出三角形的形状.
,根据平面向量的数量积运算法则可求出C的度数,进而判断出三角形的形状.
解答:根据向量的性质可得: ,
,
∴ 在∠BAC的角平分线上(设角平分线为AD),
在∠BAC的角平分线上(设角平分线为AD),
∵ ,
,
∴AD⊥BC,
∴AB=AC,即三角形为等腰三角形,
∴∠B=∠C,
又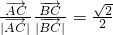 ,且
,且  ,
,
∴∠C=45°,
∴∠A=90°,
则三角形为等腰直角三角形.
故选D
点评:此题考查了三角形形状的判断,涉及的知识有:平面向量的加法的四边形法则,向量的数量积的运算,全等三角形的判定与性质,以及等腰直角三角形的判定,熟练掌握平面向量的数量积运算法则是解本题的关键.
分析:根据任意一向量与该向量的模的比值都是单位向量,可得:
 ,进而得到
,进而得到 在∠BAC的角平分线上(设角平分线为AD),再根据两向量的数量积为0,可得两向量垂直可得AD与BC垂直,根据三角形的全等,可得AB=AC,即三角形为等腰三角形,同时由
在∠BAC的角平分线上(设角平分线为AD),再根据两向量的数量积为0,可得两向量垂直可得AD与BC垂直,根据三角形的全等,可得AB=AC,即三角形为等腰三角形,同时由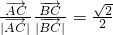 及
及 ,根据平面向量的数量积运算法则可求出C的度数,进而判断出三角形的形状.
,根据平面向量的数量积运算法则可求出C的度数,进而判断出三角形的形状.解答:根据向量的性质可得:
 ,
,∴
 在∠BAC的角平分线上(设角平分线为AD),
在∠BAC的角平分线上(设角平分线为AD),∵
 ,
,∴AD⊥BC,
∴AB=AC,即三角形为等腰三角形,
∴∠B=∠C,
又
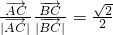 ,且
,且  ,
,∴∠C=45°,
∴∠A=90°,
则三角形为等腰直角三角形.
故选D
点评:此题考查了三角形形状的判断,涉及的知识有:平面向量的加法的四边形法则,向量的数量积的运算,全等三角形的判定与性质,以及等腰直角三角形的判定,熟练掌握平面向量的数量积运算法则是解本题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
 和
和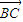 满足
满足 ,且
,且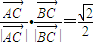 ,则△ABC为( )
,则△ABC为( )