题目内容
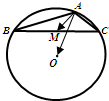如图，O为△ABC的外心，AB=4，AC=2，∠BAC为钝角，M是边BC的中点，则| AM |
| AO |
分析：取AB、AC的中点D、E，可知OD⊥AB，OE⊥AC，所求
•
=
•
+
•
，由数量积的定义结合图象可得
•
=|
|2，
•
=|
|2，代值即可．
| AM |
| AO |
| AD |
| AO |
| AE |
| AO |
| AD |
| AO |
| AD |
| AE |
| AO |
| AE |
解答：
解：（如图）取AB、AC的中点D、E，可知OD⊥AB，OE⊥AC
∵M是边BC的中点，∴
=
(
+
)
∴
•
=
(
+
)•
=
•
+
•
，
=
•
+
•
，
由数量积的定义可得
•
=|
||
|cos＜
，
＞，
而|
|cos＜
，
＞=|
|，故
•
=|
|2=4；
同理可得
•
=|
|2=1，
故
•
+
•
=5，
故选D
解：（如图）取AB、AC的中点D、E，可知OD⊥AB，OE⊥AC∵M是边BC的中点，∴
| AM |
| 1 |
| 2 |
| AB |
| AC |
∴
| AM |
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| 1 |
| 2 |
| AB |
| AO |
| 1 |
| 2 |
| AC |
| AO |
=
| AD |
| AO |
| AE |
| AO |
由数量积的定义可得
| AD |
| AO |
| AD |
| AO |
| AD |
| AO |
而|
| AO |
| AD |
| AO |
| AD |
| AD |
| AO |
| AD |
同理可得
| AE |
| AO |
| AE |
故
| AD |
| AO |
| AE |
| AO |
故选D
点评：本题为向量数量积的运算，数形结合并熟练应用数量积的定义是解决问题的关键，属中档题．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
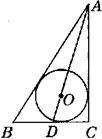如图，⊙O为△ABC的内切圆，∠C=90度，OA的延长线交BC于点D，AC=4，CD=1，则⊙O的半径等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
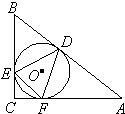
（2013•兰州一模）选修4-1：《几何证明选讲》
为
△ABC的外接圆，AB=AC，过点A的直线交⊙O于D，交BC延长线
于F，DE是BD的延长线，连接CD。