题目内容
5.有下列命题:①双曲线$\frac{x^2}{25}-\frac{y^2}{9}=1$与椭圆$\frac{x^2}{35}+{y^2}=1$有相同的焦点;②“-$\frac{1}{2}$<x<0”是“2x2-5x-3<0”必要不充分条件;
③若$\overrightarrow a$、$\overrightarrow b$共线,则$\overrightarrow a$、$\overrightarrow b$所在的直线平行;
④等轴双曲线的离心率是$\sqrt{2}$;
⑤?x∈R,x2-3x+3≠0.
其中是真命题的有:①④⑤.
分析 ①求出双曲线和椭圆的焦点进行判断.
②根据充分条件和必要条件的定义进行判断即可.
③根据向量关系与直线的位置关系进行判断.
④根据等轴双曲线的定义进行判断.
⑤根据一元二次方程的根与判别式△的关系进行求解.
解答 解:①双曲线$\frac{x^2}{25}-\frac{y^2}{9}=1$中a2=25,b2=9,则c2=25+9=34,则c=$\sqrt{34}$,对应的焦点坐标为($\sqrt{34}$,0),(-$\sqrt{34}$,0),
椭圆$\frac{x^2}{35}+{y^2}=1$中a2=35,b2=1,则c2=35-1=34则c=$\sqrt{34}$,对应的焦点坐标为($\sqrt{34}$,0),(-$\sqrt{34}$,0),
双曲线和椭圆的焦点相同;故①正确,
②由2x2-5x-3<0得-$\frac{1}{2}$<x<3,
则“-$\frac{1}{2}$<x<0”是“2x2-5x-3<0”充分不必要条件;故②错误,
③若$\overrightarrow a$、$\overrightarrow b$共线,则$\overrightarrow a$、$\overrightarrow b$所在的直线平行或重合,故③错误;
④等轴双曲线的离心率是$\sqrt{2}$正确,故④正确;
⑤∵判别式△=9-4×3=9-12=-3<0,
∴?x∈R,x2-3x+3≠0成立,故⑤正确,
故正确的命题是①④⑤,
故答案为:①④⑤
点评 本题主要考查的真假判断,涉及圆锥曲线的定义和性质以及充分条件和必要条件的判断,涉及的知识点较多.

练习册系列答案
相关题目
20.已知焦点在y轴上的双曲线C的一条渐近线与直线$l:x+\sqrt{3}y=0$垂直,且C的一个焦点到l的距离为3,则C的标准方程为( )
| A. | $\frac{y^2}{9}-\frac{x^2}{3}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{3}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{6}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{6}=1$ |
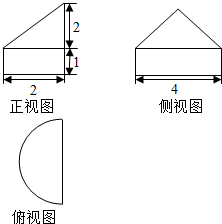
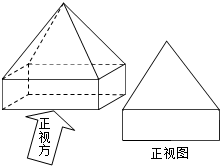
17.如图所示的一个几何体及其正视图如图,则其俯视图是( )

| A. |  | B. | 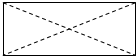 | C. | 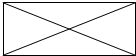 | D. | 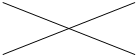 |
15.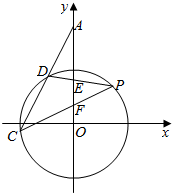 如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
 如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |