题目内容
13.如图1,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为$\frac{{\sqrt{6}}}{3}$,求三棱锥F-BDE的体积.
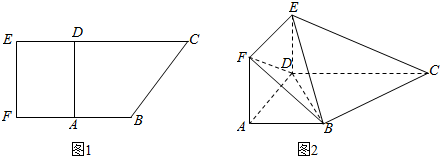
分析 (1)证明ED⊥BC,BC⊥BD,ED∩BD=D,即可证明BC⊥平面BDE;
(3)由(1)知,平面DBE⊥平面BCE,作DH⊥BE,则DH⊥平面BCE,求出高DE,转换底面即可求三棱锥F-BDE的体积.
解答  (1)证明:在正方形ADEF中,ED⊥AD.
(1)证明:在正方形ADEF中,ED⊥AD.
又∵平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
∴ED⊥平面ABCD,则ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,∠BDC=45°,可得BC=$\sqrt{2}$.
在△BCD中,BD=BC=$\sqrt{2}$,CD=2,∴BD2+BC2=CD2.
∴BC⊥BD.
故BC⊥平面BDE;
(2)解:由(1)知,平面DBE⊥平面BCE,作DH⊥BE,则DH⊥平面BCE,∴DH=$\frac{\sqrt{6}}{3}$,
△BDE中,由等面积可得$\sqrt{2}$•DE=$\frac{\sqrt{6}}{3}$•$\sqrt{D{E}^{2}+2}$
∴DE=1,
∴VF-BDE=VB-DEF=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
点评 本题考查平面与平面垂直的性质,考查线面垂直的判定,考查三棱锥F-BDE的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.函数f(x)=sinπx+2xcosx的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
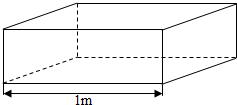 用某种型号的钢板焊接一个长为1m的无盖长方体容器(接缝忽略不计他),要求其容积为2m3,则至少需要这种型号的钢板8m2.
用某种型号的钢板焊接一个长为1m的无盖长方体容器(接缝忽略不计他),要求其容积为2m3,则至少需要这种型号的钢板8m2. 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为$\sqrt{7}$m,求证:
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为$\sqrt{7}$m,求证: