题目内容
7.下列命题:①函数y=-sin(kπ+x)(k∈Z)是奇函数;
②函数f(x)=sin|x|是最小正周期为π的周期函数;
③设θ为第二象限角,则tanθ>cos$\frac{θ}{2}$,且sin$\frac{θ}{2}$>cos$\frac{θ}{2}$
④函数y=cos2x+sinx的最小值为-1
其中真命题的序号是①④((写出所有正确命题的编号))
分析 依次分析命题:①根据奇函数的定义进行判断;
②结合函数y=sin|x|的图象可判断;
③首先推知$\frac{θ}{2}$所在的象限,然后再来比较它们的大小;
④根据sinx∈[-1,1]、y=-(sinx-$\frac{1}{2}$)2+$\frac{5}{4}$,利用二次函数的性质求得它的最小值.
解答 解:①函数y=-sin(kπ+x)(k∈Z)=$\left\{\begin{array}{l}{sinx,k是奇数}\\{-sinx,k是偶数}\end{array}\right.$,为奇函数,成立;
②函数y=sin|x|得图象如图所示,由图象可知函数不是周期函数,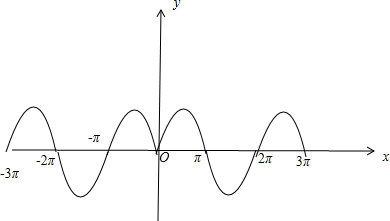
故②不成立;
③∵θ是第二象限的角,即2kπ+$\frac{π}{2}$<θ<2kπ+π,k∈z,可得kπ+$\frac{π}{4}$<$\frac{θ}{2}$<kπ+$\frac{π}{2}$,
∴$\frac{θ}{2}$可能在第一或第三象限,
∴无法比较tanθ与cos$\frac{θ}{2}$,sin$\frac{θ}{2}$与cos$\frac{θ}{2}$的大小,故③不一定成立;
④函数y=cos2x+sinx=-sin2x+sinx+1=-(sinx-$\frac{1}{2}$)2+$\frac{5}{4}$,再根据sinx∈[-1,1],
可得当sinx=$\frac{1}{2}$时,函数取得最大值为$\frac{5}{4}$,当sinx=-1时,函数取得最小值为-1,
故④成立.
综上所述,正确的结论是:①④.
故答案是:①④.
点评 本题考查命题的真假判断和应用,解题时要注意函数的连续性和极限的灵活运用.

练习册系列答案
相关题目
18.极坐标系中,曲线θ=$\frac{2π}{3}$与ρ=6sinθ的两个交点之间的距离为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |