题目内容

9个相同的小球放入标号为1、2、3的3个小盒子中，要求每个盒子都不空，共有方法总数为       ．
21
解：由题意知本题采用隔板法，
将9个小球排成一排，插入2块隔板，
隔板将9个元素分成3部分，每一部分至少一个，
∴共有分法=21（种）．
练习册系列答案
相关题目
将5名护士分配到某市的3家医院，每家医院至少分到一名护士的分配方案有（  ）
A．30种B．150种C．180种D．60种
如图：A、B、C、D、E五个区域可用红、蓝、黄、白、绿五种颜色中的某一种着色.要求相邻的区域着不同的颜色，则不同的着色方式种数有
A. 16                  B.  120            C.  360            D.  540
A
B
C
D
E
 
 
 
现有4个同学去看电影，他们坐在了同一排，且一排有6个座位．问：
（1）所有可能的坐法有多少种？
（2）此4人中甲，乙两人相邻的坐法有多少种？
（3）所有空位不相邻的坐法有多少种？（结果均用数字作答）
（12分）将4个编号为1,2,3,4的不同小球全部放入4个编号为1,2,3,4的4个不同盒子中，求：
（1）每盒至少一个球，有多少种放法？
（2）恰好有一个空盒，有多少种放法？
（3）每盒放一个球，并且恰好有一个球的编号与盒子的编号相同，有多少种放法？
（4）把已知中4个不同的小球换成四个完全相同的小球（无编号），其余条件不变，恰有一个空盒，有多少种放法？
由0、1、2、3组成个位数字不是1的没有重复数字的四位数共有           个．
（本小题满分10分）
(1) 
（2）解方程：　　
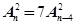
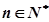
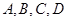从6名销售人员中选4名分别派驻到四个城市，要求每个城市都有人到，每人只到一城市，且这6名销售人员中的甲、乙两人不去A城市，则不同的选择方案共有         种（用数字表示结果）
.（用数字作答）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网