题目内容
已知集合M={x|2x≥ },N={y|x2+y2=4,x∈R,y∈R}︳,则M∩N
},N={y|x2+y2=4,x∈R,y∈R}︳,则M∩N
- A.{-2,1}
- B.
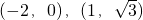
- C.∅
- D.N
D
分析:根据指数不等式求得集合M=[-2,+∞),根据圆的有界性,求得N=[-2,2],根据集合交集的求法求得M∩N.
解答:解;集合M={x|2x≥ }={x|2x≥2-2}={x|x≥-2}=[-2,+∞),
}={x|2x≥2-2}={x|x≥-2}=[-2,+∞),
N={y|x2+y2=4,x,y∈R}=[-2,2],
∴M∩N=[-2,2]=N,
故选D.
点评:此题是个基础题.考查交集及其运算,以及不等式的解法和圆的有界性,同时考查学生的计算能力.
分析:根据指数不等式求得集合M=[-2,+∞),根据圆的有界性,求得N=[-2,2],根据集合交集的求法求得M∩N.
解答:解;集合M={x|2x≥
 }={x|2x≥2-2}={x|x≥-2}=[-2,+∞),
}={x|2x≥2-2}={x|x≥-2}=[-2,+∞),N={y|x2+y2=4,x,y∈R}=[-2,2],
∴M∩N=[-2,2]=N,
故选D.
点评:此题是个基础题.考查交集及其运算,以及不等式的解法和圆的有界性,同时考查学生的计算能力.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目