题目内容
P为椭圆
＝1(a＞b＞0)上一点，F1为它的一个焦点，求证：以PF1为直径的圆与以长轴为直径的圆相切．
＝1(a＞b＞0)上一点，F1为它的一个焦点，求证：以PF1为直径的圆与以长轴为直径的圆相切．设PF1的中点为M，则两圆圆心之间的距离为
｜OM｜＝
｜PF2｜＝ (2a－｜PF1｜)＝a－｜PF1｜．
即两圆圆心之间的距离等于两圆半径之差，∴两圆内切．即以PF1为直径的圆与以长轴为直径的圆相切．
｜OM｜＝
｜PF2｜＝ (2a－｜PF1｜)＝a－｜PF1｜．即两圆圆心之间的距离等于两圆半径之差，∴两圆内切．即以PF1为直径的圆与以长轴为直径的圆相切．
同答案
练习册系列答案
相关题目
,讨论方程表示的曲线的形状
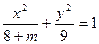的离心率是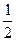
，则两准线间的距离是 ．
，－
)
，
，
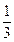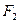分别为其左、右焦点，
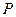为椭圆上任意一点，
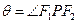，求
的最大值及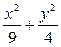
＝1上一点，F1、F2是椭圆的两个焦点，则cosF1PF2的最小值是( )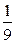
（
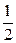
），过椭圆中心O作互相垂直的两条弦AC、BD，设点A、B的离心角分别为
和
，求
的取值范围。