题目内容
定义在（-∞，+∞）上的偶函数f（x）满足f（x+2）=f（x），当x∈[0，1]时，f（x）=10x-1，下面关于函数f（x）的判断：①当x∈[-1，0]时，f（x）=10-x-1；
②函数f（x）的图象关于直线x=1对称；
③对任意x1，x2∈（1，2），满足（x2-x1）（f（x2）-f（x1））＜0；
④当x∈[2k，2k+1]，k∈Z时，f（x）=10x-2k-1．其中正确判断的个数为（ ）
A．1
B．2
C．3
D．4
【答案】分析：x∈[0，1]时的解析式知道，利用偶函数，可先求得x∈[-1，0]时的解析式，又由f（x+2）=f（x）说明f（x）是周期为2的周期函数，则R上的解析式均可求出．可结合图象求解．
解答：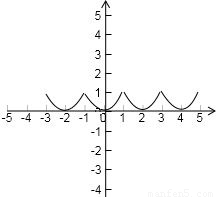
解：由题意可知f（x）的图象如图所示：
①当x∈[-1，0]时，-x∈[0，1]，则f（-x）=10-x-1，因为f（x）为偶函数，所以f（x）=f（-x）=10-x-1，故①正确；
②正确；③x∈（1，2）时，f（x）为减函数，故③正确；
④当x∈[2k，2k+1]，k∈Z时，x-2k∈[0，1]，所以f（x-2k）=10x-2k-1，
由f（x+2）=f（x）可知，f（x）是周期为2的周期函数，所以f（x）=f（x-2k）=10x-2k-1，④正确．
故选D．
点评：本题考查函数性质的综合应用，函数解析式的求解，综合性较强．
解答：
解：由题意可知f（x）的图象如图所示：①当x∈[-1，0]时，-x∈[0，1]，则f（-x）=10-x-1，因为f（x）为偶函数，所以f（x）=f（-x）=10-x-1，故①正确；
②正确；③x∈（1，2）时，f（x）为减函数，故③正确；
④当x∈[2k，2k+1]，k∈Z时，x-2k∈[0，1]，所以f（x-2k）=10x-2k-1，
由f（x+2）=f（x）可知，f（x）是周期为2的周期函数，所以f（x）=f（x-2k）=10x-2k-1，④正确．
故选D．
点评：本题考查函数性质的综合应用，函数解析式的求解，综合性较强．
练习册系列答案
相关题目
已知函数f（x）是定义在R上的奇函数，其最小正周期为3，且x∈(-
，0)时，f（x）=2-x+1则f（8）=（ ）
| 3 |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|