题目内容
19．函数f（x）=$\frac{1}{2}$（1+cos2x）sin2x，x∈R是（ ）| A． | 最小正周期为π的奇函数 | B． | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C． | 最小正周期为π的偶函数 | D． | 最小正周期为$\frac{π}{2}$的偶函数 |
分析 由三角函数恒等变换化简函数解析式可得：f（x）=$\frac{1}{8}$-$\frac{1}{8}$cos4x．，由周期公式可求得T，由余弦函数的图象和性质可知函数为偶函数．
解答 解：∵f（x）=$\frac{1}{2}$（1+cos2x）sin2x=cos2xsin2x=$\frac{1}{4}$sin22x=$\frac{1}{4}$×$\frac{1-cos4x}{2}$=$\frac{1}{8}$-$\frac{1}{8}$cos4x．
∴由周期公式可得：T=$\frac{2π}{4}$=$\frac{π}{2}$，由余弦函数的图象和性质可知函数为偶函数．
故选：D．
点评 本题主要考查了三角函数恒等变换的应用，考查了三角函数的周期性及其求法，正弦函数的奇偶性，属于基本知识的考查．
练习册系列答案
相关题目
9．三条不重合的直线a，b，c及三个不重合的平面α，β，γ，下列命题正确的是（ ）
| A． | 若a∥α，a∥β，则α∥β | B． | 若α∩β=a，α⊥γ，β⊥γ，则a⊥γ | ||
| C． | 若a?α，b?α，c?β，c⊥a，c⊥b，则α⊥β | D． | 若α∩β=a，c?γ，c∥α，c∥β，则a∥γ |
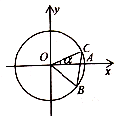如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（$\frac{12}{13}$，-$\frac{5}{13}$），∠AOC=α，若|BC|=1，则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$．