Question

【题目】已知函数f（x）=loga（x2﹣2），若f（2）=1
（1）求a的值；
（2）求f（3 ）的值；
（3）解不等式f（x）＜f（x+2）．

Answer 1

【答案】
（1）解：∵f（x）=loga（x2﹣2），f（2）=1

∴f（2）=loga2=1

解得a=2

（2）解：由（1）可知f（x）=log2（x2﹣2），

∴f（3 ）=log2（（3 ）2﹣2）=log216=4

（3）解：∵f（x）＜f（x+2）

∴log2（x2﹣2）＜log2（（x+2）2﹣2），

即 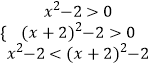解得x＞

∴不等式的解集为{x|x＞ }

【解析】（1）将x=2代入函数f（x）=loga（x2﹣2），根据对数的运算法则可求出a的值；（2）由（1）可得函数的解析式，将x=3 代入解析式，化简可得结论；（3）根据不等式f（x）＜f（x+2）建立关系式，注意对数函数的真数大于0这一条件．
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识，掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集，以及对函数的值的理解，了解函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．