题目内容
【题目】如图,AOB是一块半径为r的扇形空地,![]() .某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若
.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若![]() ,设
,设![]()
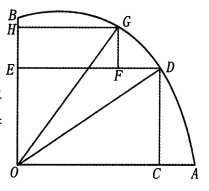
(Ⅰ)记活动场地与停车场占地总面积为![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅱ)当![]() 为何值时,可使活动场地与停车场占地总面积最大.
为何值时,可使活动场地与停车场占地总面积最大.
【答案】(Ⅰ)![]() 其中
其中![]() ;
;
(Ⅱ)![]() 时,可使活动场地与停车场占地总面积最大.
时,可使活动场地与停车场占地总面积最大.
【解析】
(Ⅰ)由题意求得矩形![]() 和矩形
和矩形![]() 的面积(Ⅱ)求
的面积(Ⅱ)求![]() 的导数
的导数![]() ,利用
,利用![]() ,
,
判断![]() 的单调性,求最大值即可.
的单调性,求最大值即可.
![]() Ⅰ
Ⅰ![]() 由题意得,在矩形OCDE中,
由题意得,在矩形OCDE中,![]() ,
,![]() ,
,![]() ,
,
![]() 矩形OCDE的面积为
矩形OCDE的面积为![]() ;
;
又![]() ,四边形EFGH是矩形,
,四边形EFGH是矩形,![]() ,
,![]() ,
,
![]() ;
;
![]() 矩形EFGH的面积为
矩形EFGH的面积为![]() ,
,
 ,其中
,其中![]() ;
;
![]() Ⅱ
Ⅱ![]() 由题意知,
由题意知,![]() ,
,
令![]() ,得
,得![]() ,
,
解得![]() ,或
,或![]() 不合题意,舍去
不合题意,舍去![]() ;
;
令![]() ,则
,则![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
![]() 当
当![]() 时,
时,![]() 取得最大值;
取得最大值;
即![]() 时,可使活动场地与停车场占地总面积最大.
时,可使活动场地与停车场占地总面积最大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某果农从经过筛选(每个水果的大小最小不低于50克,最大不超过100克)的10000个水果中抽取出100个样本进行统计,得到如下频率分布表:
级别 | 大小(克) | 频数 | 频率 |
一级果 |
| 5 | 0.05 |
二级果 |
|
| |
三级果 |
| 35 |
|
四级果 |
| 30 | |
五级果 |
| 20 | |
合计 | 100 |
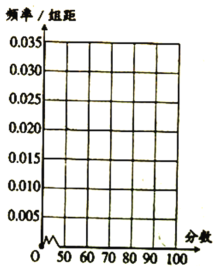
请根据频率分布表中所提供的数据,解得下列问题:
(1)求![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)若从四级果,五级果中按分层抽样的方法抽取5个水果,并从中选出2个作为展品,求2个展品中仅有1个是四级果的概率;
(3)若将水果作分级销售,预计销售的价格![]() 元/个与每个水果的大小
元/个与每个水果的大小![]() 克关系是:
克关系是: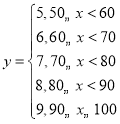 ,则预计10000个水果可收入多少元?
,则预计10000个水果可收入多少元?


