题目内容
已知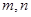 是两条异面直线,点
是两条异面直线,点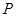 是直线
是直线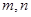 外的任一点,有下面四个结论:
外的任一点,有下面四个结论:
①过点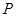 一定存在一个与直线
一定存在一个与直线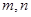 都平行的平面。
都平行的平面。
②过点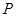 一定存在一条与直线
一定存在一条与直线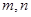 都相交的直线。
都相交的直线。
③过点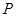 一定存在一条与直线
一定存在一条与直线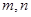 都垂直的直线。
都垂直的直线。
④过点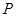 一定存在一个与直线
一定存在一个与直线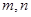 都垂直的平面。则四个结论中正确的个数为( )
都垂直的平面。则四个结论中正确的个数为( )
 是两条异面直线,点
是两条异面直线,点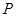 是直线
是直线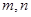 外的任一点,有下面四个结论:
外的任一点,有下面四个结论:①过点
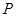 一定存在一个与直线
一定存在一个与直线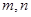 都平行的平面。
都平行的平面。②过点
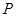 一定存在一条与直线
一定存在一条与直线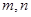 都相交的直线。
都相交的直线。③过点
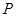 一定存在一条与直线
一定存在一条与直线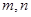 都垂直的直线。
都垂直的直线。④过点
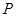 一定存在一个与直线
一定存在一个与直线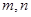 都垂直的平面。则四个结论中正确的个数为( )
都垂直的平面。则四个结论中正确的个数为( )| A.1 | B.2 | C.3 | D.4 |
A
专题:综合题;阅读型.
分析:对于①②过直线m存在一个与直线n平行的平面,当点P在这个平面内时,就不满足结论,对于③可将直线m和n平移到一起,确定一个平面,过点P作平面的垂线即可,对于④利用反证法即可.
解答:解:①错.因为过直线m存在一个与直线n平行的平面,当点P在这个平面内时,就不满足结论.
②错.因为过直线m存在一个与直线n平行的平面,当点P在这个平面内时,就不满足结论.
③对,将直线m和n平移到一起,确定一个平面,过点P作平面的垂线即可;
④错.若结论成立,则有m∥n,而m与n不一定平行;
故选A
点评:本题主要考查了空间中直线与平面之间的位置关系,以及反证法的应用,同时考查了推理能力,属于基础题.

练习册系列答案
相关题目
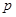 :
: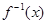 是
是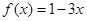 的反函数,且
的反函数,且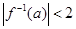 ;命题
;命题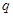 :集合
:集合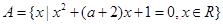 ,
,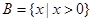 ,且
,且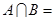 Ф.
Ф.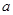 的取值范围。
的取值范围。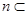 平面β,下列说法正确的有
平面β,下列说法正确的有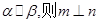 ②若
②若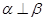 ,则m//n
,则m//n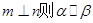
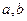 都是偶数,则
都是偶数,则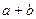 是偶数”的否命题是
是偶数”的否命题是 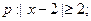 命题
命题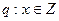 .如果
.如果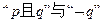 同时为假命题,则满足条件的
同时为假命题,则满足条件的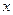 的集合为 ▲ .
的集合为 ▲ .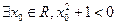 ”
” 的否定是()
的否定是()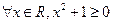
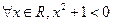
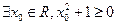
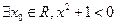
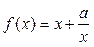 在区间[1,2]上单调递增;
在区间[1,2]上单调递增; 命题Q:不等式
命题Q:不等式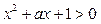 对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是 ( )
对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是 ( )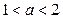 B
B 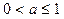

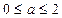 D
D 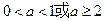
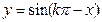
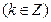 为奇函数;
为奇函数;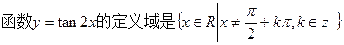 ;
;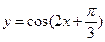 的图象的一条对称轴为
的图象的一条对称轴为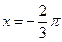 ;
;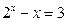 的实根个数为1个。 其中正确结论的序号为
的实根个数为1个。 其中正确结论的序号为  ).
). ①“若对所有满足
①“若对所有满足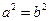 的
的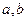 ,都有
,都有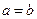 ”的否命题;
”的否命题;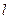 的方向向量为
的方向向量为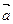 =(1,
=(1,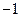 ,2),平面
,2),平面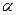 的法向量为
的法向量为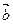 =(-2,0,1),
=(-2,0,1),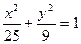 与曲线
与曲线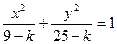 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点;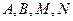 是空间四点,若
是空间四点,若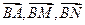 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么