题目内容
【题目】已知f（x）为二次函数，且
．
（1）求f（x）的表达式；
（2）判断函数
在（0，+∞）上的单调性，并证明．
【答案】（1）
；（2）增函数，证明见解析．
【解析】
（1）利用题中所给的条件，先设出函数的解析式，利用
，将式子化为恒等式，利用对应项系数相等，得到方程组，求得结果；
（2）先化简函数解析式，利用单调性的定义，证明得到函数的单调性，得到结果.
（1）设f（x）=ax2+bx+c（a≠0），
由条件得：a（x+1）2+b（x+1）+c+a（x﹣1）2+b（x﹣1）+c=2x2﹣4x，
从而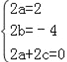
， 解得：
，
所以f（x）=x2﹣2x﹣1；
（2）函数g（x）=
在（0，+∞）上单调递增．
理由如下：g（x）==
，
设设任意x1，x2∈（0，+∞），且x1＜x2，
则g（x1）﹣g（x2）=
﹣（
）=（x1﹣x2）（1+
），
∵x1，x2∈（0，+∞），且x1＜x2，
∴x1﹣x2＜0，1+＞0，
∴g（x1）﹣g（x2）＜0，即g（x1）＜g（x2），
所以函数g（x）=
在（0，+∞）上单调递增．
练习册系列答案
阅读快车系列答案
相关题目
