Question

（2013•徐州三模）已知一块半径为r的残缺的半圆形材料ABC，O为半圆的圆心，OC=

1

2

r，残缺部分位于过点C的竖直线的右侧．现要在这块材料上截出一个直角三角形，有两种设计方案：如图甲，以BC为斜边；如图乙，直角顶点E在线段OC上，且另一个顶点D在

AB

上．要使截出的直角三角形的面积最大，应该选择哪一种方案？请说明理由，并求出截得直角三角形面积的最大值．

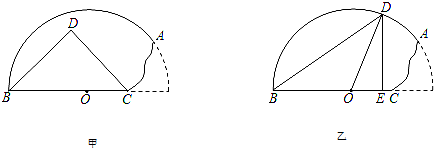
Answer 1

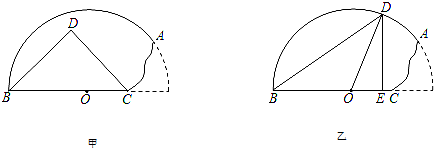
分析：在图形甲中，BC的长度为

3r

2

，设出∠DBC=α，把BD和DC都用r和角α表示，利用三角函数求直角三角形BDC面积的最大值；在图形乙中，设出∠DOE=θ，利用平面几何知识得到角θ的范围，把DE和BE用r和θ表示，写出三角形BED的面积后，利用导数分析单调性，由单调性求最值，最后比较两种情况下面积最大值的大小．

解答：解：如图甲，

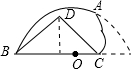
设∠DBC=α（0＜α＜

π

2

），
则BD=

3r

2

cosα，DC=

3r

2

sinα，
所以S△BDC=

1

2

BD•DC=

1

2

•

3r

2

cosα•

3r

2

sinα
=

9

16

r2sin2α≤

9

16

r2，
当且仅当α=

π

4

时取等号，
此时点D到BC的距离为

3

4

r，可以保证点D在半圆形材料ABC内部，
因此按照图甲方案得到直角三角形的最大面积为

9

16

r2．   
如图乙，

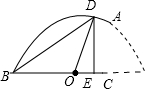
设∠EOD=θ，则OE=rcosθ，DE=rsinθ，
所以S△BDE=

1

2

r2(1+cosθ)sinθ，θ∈[

π

3

，

π

2

]．
设f(θ)=

1

2

r2(1+cosθ)sinθ，则f′(θ)=

1

2

r2(1+cosθ)(2cosθ-1)，
当θ∈[

π

3

，

π

2

]时，f'（θ）≤0，所以θ=

π

3

时，即点E与点C重合时，△BDE的面积最大值为

3 3

8

r2． 
因为

3 3

8

r2＞

9

16

r2，
所以选择图乙的方案，截得的直角三角形面积最大，最大值为

3 3

8

r2．

点评：本题考查了导数在最大值和最小值中的应用，考查了利用三角函数求几何图形的面积，解答此题的关键是把三角形的面积用变量角表示，图形乙中对角的范围的分析不可忽视，此题属中档题．