Question

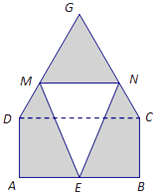
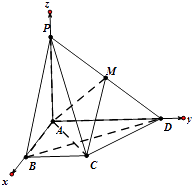
【题目】如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，AB⊥AD，BC= ，AB=1，BD=PA=2，M 为PD的中点．

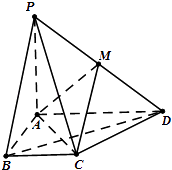
（1）求异面直线BD与PC所成角的余弦值；
（2）求二面角A﹣MC﹣D的平面角的余弦值．

Answer 1

【答案】
（1）解：∵PA⊥平面ABCD，AB平面ABCD，AD平面ABCD，

∴PA⊥AB，PA⊥AD．又AD⊥AB，如图，以AB，AD，AP所在直线为x轴、y轴、z轴建立空间直角坐标系．

根据条件得AD= ，∴B（1，0，0），D（0， ，0），C ，P（0，0，2），

则 =（﹣1， ，0）， = ．

设异面直线BD，PC所成的角为θ，

则cos θ=|cos＜ ＞|= = = ．

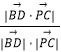即异面直线BD与PC所成角的余弦值为 ．

（2）解：设平面AMC的一个法向量为n1=（x1，y1，z1）， ，

则n1⊥ ，∴n1 =（x1，y1，z1） = ，

又n1⊥ ，∴n1 =（x1，y1，z1） = ，

取y1=- ，得x1=2，z1= ，故n1=（2，- ， ），

同理可得平面BMC的一个法向量n2=（1， ， ），

∵cos＜n1，n2＞= ，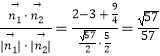

∴二面角A﹣MC﹣D的平面角的余弦值为 ．

【解析】（1）建立空间直角坐标系，利用向量的夹角公式即可得出异面直线所成的角．（2）利用法向量的性质、线面垂直的性质、向量的夹角公式即可得出．
【考点精析】根据题目的已知条件，利用异面直线及其所成的角的相关知识可以得到问题的答案，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．