题目内容
【题目】已知等差数列 
中,公差 
, 
，且 
成等比数列.
（1）求数列 的通项公式；
（2）若 
为数列 
的前 
项和，且存在 
，使得 
成立，求实数 
的取值范围.
【答案】
（1）
由题意可得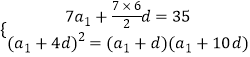 
即 
又因为d≠0，所以 
，所以 
.
（2）
解：因为 
= 
，所以 
因为存在 
使得 
成立.
又 
， 
（当且仅当n=2时取等号），
所以 
，即实数 
的取值范围是 
.
【解析】本题主要考查等差数列的通项公式、数列求和、等比数列的性质等基础知识，意在考查基本运算能力．
【考点精析】根据题目的已知条件，利用等差数列的通项公式（及其变式）和数列的前n项和的相关知识可以得到问题的答案，需要掌握通项公式：
或
；数列{an}的前n项和sn与通项an的关系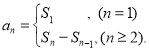
．
练习册系列答案
相关题目
