题目内容
4．已知f（x）、g（x）均为[-1，3]上连续不断的曲线，根据下表能判断方程f（x）=g（x）有实数解的区间是（ ）| x | -1 | 0 | 1 | 2 | 3 |
| f（x） | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g（x） | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A． | （-1，0） | B． | （1，2） | C． | （0，1） | D． | （2，3） |
分析 设h（x）=f（x）-g（x），利用h（0）=f（0）-g（0）=-0.44＜0，h（1）=f（1）-g（1）=0.532＞0，即可得出结论．
解答 解：设h（x）=f（x）-g（x），则
∵h（0）=f（0）-g（0）=-0.44＜0，h（1）=f（1）-g（1）=0.532＞0，
∴h（x）的零点在区间（0，1），
故选：C．
点评 本题考查函数的零点，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
15．设等差数列{an}，{bn}的前n项和分别为Sn，Tn，若$\frac{a_n}{b_n}=\frac{2n-1}{n+1}$，则$\frac{{{S_{11}}}}{{{T_{11}}}}$=（ ）
| A． | $\frac{7}{4}$ | B． | $\frac{11}{7}$ | C． | 2 | D． | $\frac{7}{2}$ |
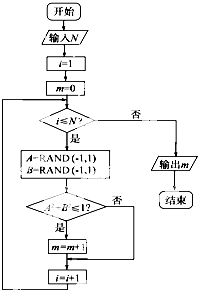如图所示的程序框图可用来估计π的值（假设函数RAND（-1，1）是产