题目内容
如图,四棱锥S-ABCD中,SD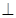 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD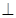 DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
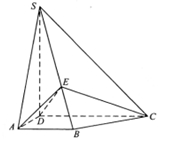
(Ⅰ)求证:无论E点取在何处恒有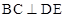 ;
;
(Ⅱ)设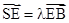 ,当平面EDC
,当平面EDC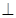 平面SBC时,求
平面SBC时,求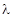 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下求二面角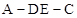 的大小.
的大小.
 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
(Ⅰ)求证:无论E点取在何处恒有
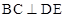 ;
;(Ⅱ)设
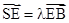 ,当平面EDC
,当平面EDC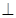 平面SBC时,求
平面SBC时,求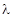 的值;
的值;(Ⅲ)在(Ⅱ)的条件下求二面角
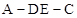 的大小.
的大小.(Ⅰ)证明见解析;(Ⅱ)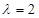 ;(Ⅲ)
;(Ⅲ)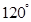 .
.
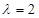 ;(Ⅲ)
;(Ⅲ)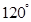 .
.试题分析:(Ⅰ)连接
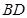 ,过点
,过点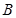 作
作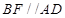 ,交
,交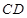 于点
于点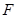 ,先证明
,先证明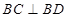 ,再由
,再由 得到
得到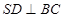 ,依据直线与平面垂直的判定定理可知,
,依据直线与平面垂直的判定定理可知,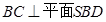 ,从而由直线与平面垂直的性质定理可得到
,从而由直线与平面垂直的性质定理可得到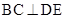 ;(Ⅱ) 分别以
;(Ⅱ) 分别以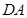 ,
,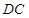 ,
,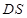 所在直线为
所在直线为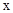 轴,
轴,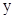 轴,
轴,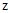 建立空间直角坐标系,根据
建立空间直角坐标系,根据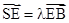 ,求得
,求得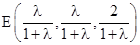 ,由
,由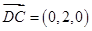 ,
,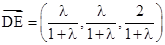 以及
以及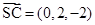 ,
,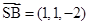 ,分别取平面
,分别取平面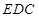 和平面
和平面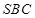 的法向量
的法向量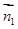 和
和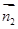 ,则由已知条件“
,则由已知条件“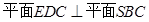 ”可得
”可得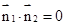 ,从而解出
,从而解出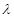 的值;(Ⅲ)当
的值;(Ⅲ)当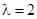 时,
时,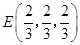 ,分别求出平面
,分别求出平面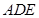 和平面
和平面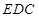 的一个法向量,求出它们的法向量的夹角,根据二面角
的一个法向量,求出它们的法向量的夹角,根据二面角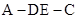 是一个钝角,那么法向量的夹角或夹角的补角即是所求的二面角.
是一个钝角,那么法向量的夹角或夹角的补角即是所求的二面角.试题解析:(Ⅰ)连接
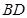 ,过点
,过点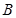 作
作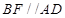 ,交
,交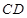 于点
于点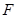 ,如图:
,如图: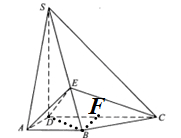
∵
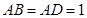 ,∴
,∴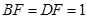 ,
,又∵
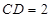 ,∴
,∴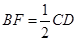 ,
,∴
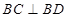 ,又
,又 ,∴
,∴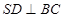 ,
,∵
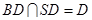 ,∴
,∴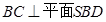 ,
,∵
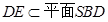 ,∴
,∴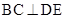 .
.(Ⅱ)分别以
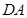 ,
,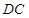 ,
,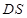 所在直线为
所在直线为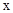 轴,
轴,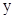 轴,
轴,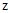 建立空间直角坐标系,如图:
建立空间直角坐标系,如图: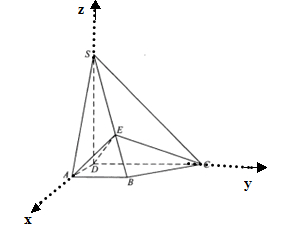
设
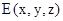 ,则
,则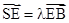
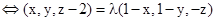
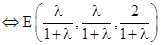 ,
,∵
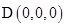 ,
,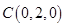 ,
,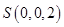 ,
,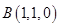 ,
,所以
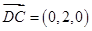 ,
,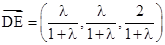 ,
,取平面
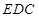 的一个法向量
的一个法向量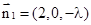 ,
,∵
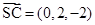 ,
,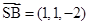 ,取平面
,取平面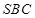 的一个法向量
的一个法向量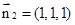 ,
,∴
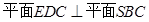
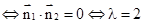 .
.(Ⅲ)当
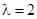 时,
时,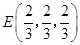 ,
,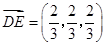 ,
,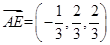 ,
,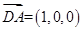 ,
,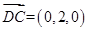 ,
,取平面
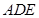 的一个法向量
的一个法向量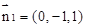 ,
,取平面
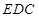 的一个法向量
的一个法向量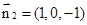 ,则
,则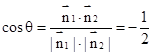 ,
,∴二面角
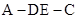 为
为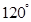 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
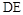
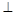 平面
平面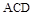 ,
,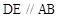 ,
,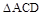 是正三角形,AD=DE
是正三角形,AD=DE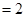 AB,且F是CD的中点.
AB,且F是CD的中点.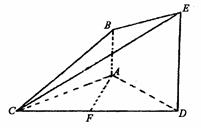
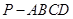 底面是平行四边形,面
底面是平行四边形,面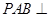 面
面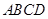 ,
,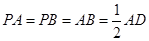 ,
,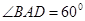 ,
,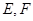 分别为
分别为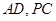 的中点.
的中点.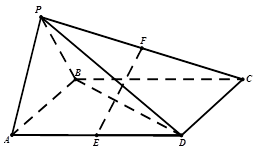
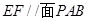
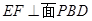
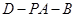 的余弦值.
的余弦值.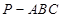 中,
中,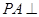 平面
平面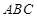 ,
,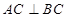 ,
, 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.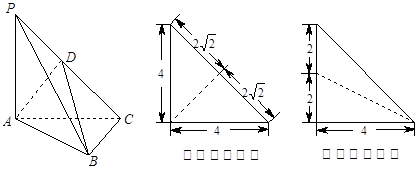
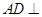 平面
平面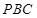 ;
;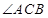 的平分线上确定一点
的平分线上确定一点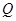 ,使得
,使得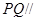 平面
平面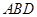 ,并求此时
,并求此时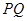 的长.
的长.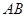 是
是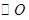 的直径,
的直径,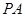 垂直于
垂直于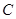 是圆周上不同于
是圆周上不同于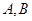 的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).
的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).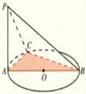
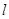 和平面
和平面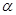 ,若
,若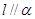 ,
,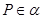 ,过点
,过点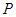 且平行于
且平行于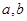 是异面直线,直线
是异面直线,直线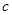 ∥直线
∥直线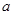 ,那么
,那么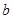 ( )
( )