题目内容
已知两点A(-1,0)、B(1,0),点P(x,y)是直角坐标平面上的动点,若将点P的横坐标保持不变、纵坐标扩大到 倍后得到点Q(x,
倍后得到点Q(x, )满足
)满足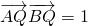 .
.
(1)求动点P所在曲线C的轨迹方程;
(2)过点B作斜率为- 的直线i交曲线C于M、N两点,且满足
的直线i交曲线C于M、N两点,且满足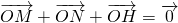 (O为坐标原点),试判断点H是否在曲线C上,并说明理由.
(O为坐标原点),试判断点H是否在曲线C上,并说明理由.
解(1)依据题意,有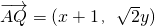 ,
,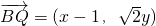 .
.
∵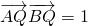 ,∴x2-1+2y2=1.
,∴x2-1+2y2=1.
∴动点P所在曲线C的轨迹方程是 +y2=1.
+y2=1.
(2)因直线l过点B,且斜率为k=- ,故有l:y=-
,故有l:y=- (x-1)
(x-1)
联立直线与椭圆,消元可得2x2-2x-1=0.
设两曲线的交点为M(x1,y1)、N(x2,y2),可得得 x1+x2=1,x1x2=- ,
,
于是 x1+x2=1,y1+y2= .
.
又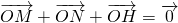 ,于是
,于是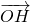 =(-x1-x2,-y1-y2),可得点H(-1,-
=(-x1-x2,-y1-y2),可得点H(-1,- ).
).
将点H(-1,- )的坐标代入曲线C的方程的左边,有
)的坐标代入曲线C的方程的左边,有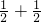 =1(=右边),即点H的坐标满足曲线C的方程.
=1(=右边),即点H的坐标满足曲线C的方程.
所以点H在曲线C上.
分析:(1)确定向量AQ,BQ的坐标,利用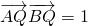 ,即可求动点P所在曲线C的轨迹方程;
,即可求动点P所在曲线C的轨迹方程;
(2)求出直线方程与椭圆联立,利用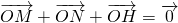 ,求得点H的坐标代入曲线C的方程,验证可得结论.
,求得点H的坐标代入曲线C的方程,验证可得结论.
点评:本题考查轨迹方程的求法,考查直线与椭圆的位置关系,考查向量知识的运用,属于中档题.
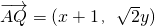 ,
,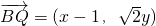 .
.∵
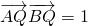 ,∴x2-1+2y2=1.
,∴x2-1+2y2=1.∴动点P所在曲线C的轨迹方程是
 +y2=1.
+y2=1.(2)因直线l过点B,且斜率为k=-
 ,故有l:y=-
,故有l:y=- (x-1)
(x-1)联立直线与椭圆,消元可得2x2-2x-1=0.
设两曲线的交点为M(x1,y1)、N(x2,y2),可得得 x1+x2=1,x1x2=-
 ,
,于是 x1+x2=1,y1+y2=
 .
.又
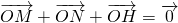 ,于是
,于是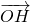 =(-x1-x2,-y1-y2),可得点H(-1,-
=(-x1-x2,-y1-y2),可得点H(-1,- ).
).将点H(-1,-
 )的坐标代入曲线C的方程的左边,有
)的坐标代入曲线C的方程的左边,有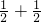 =1(=右边),即点H的坐标满足曲线C的方程.
=1(=右边),即点H的坐标满足曲线C的方程.所以点H在曲线C上.
分析:(1)确定向量AQ,BQ的坐标,利用
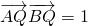 ,即可求动点P所在曲线C的轨迹方程;
,即可求动点P所在曲线C的轨迹方程;(2)求出直线方程与椭圆联立,利用
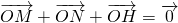 ,求得点H的坐标代入曲线C的方程,验证可得结论.
,求得点H的坐标代入曲线C的方程,验证可得结论.点评:本题考查轨迹方程的求法,考查直线与椭圆的位置关系,考查向量知识的运用,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知两点A(-1,0),B(0,2),点P是圆(x-1)2+y2=1上任意一点,则△PAB面积的最大值与最小值分别是( )
A、2,
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|