题目内容
若双曲线 的一个焦点是圆
的一个焦点是圆 的圆心,且虚轴长为
的圆心,且虚轴长为 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. |
C. | D. |
A
解析试题分析:因为圆的方程 ,利用配方法化为圆的标准方程为
,利用配方法化为圆的标准方程为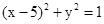 ,可知圆心(5,0),半径为1,那么可知双曲线的焦点为(5,0),则C=5,又以为虚轴长为2b=6,b=3,结合勾股定理
,可知圆心(5,0),半径为1,那么可知双曲线的焦点为(5,0),则C=5,又以为虚轴长为2b=6,b=3,结合勾股定理 ,故选A.
,故选A.
考点:本试题主要是考查了圆和双曲线的方程与性质的综合运用。
点评:解决该试题的关键是得到圆的圆心坐标,从而得到双曲线的焦点,即可知c的值,然后结合虚轴长得到b的值,进而结合a,b,c的关系得到离心率。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
若圆 :
: 关于直线
关于直线 对称,则
对称,则 的最小值是( )
的最小值是( )
| A.2 | B. | C. | D. |
若直线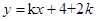 与曲线
与曲线 有两个交点,则
有两个交点,则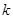 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知焦点在 轴上的椭圆的离心率为
轴上的椭圆的离心率为 ,它的长轴长等于圆
,它的长轴长等于圆 的半径,则椭圆的标准方程是( )
的半径,则椭圆的标准方程是( )
A. | B. | C. | D. |
圆 与圆
与圆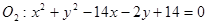 的位置关系是( )
的位置关系是( )
| A.相离 | B.内含 | C.外切 | D.内切 |
若直线y=x-2被圆 所截得的弦长为
所截得的弦长为 ,则实数
,则实数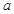 的值为( )
的值为( )
A.-1或 | B.1或3 | C.-2或6 | D.0或4 |
圆 的圆心坐标为( )
的圆心坐标为( )
A. | B. | C. | D. |
过点 作直线
作直线 与圆
与圆 相交于
相交于 两点,那么
两点,那么 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
直线 截圆
截圆 得到的弦长为( )
得到的弦长为( )
A. | B. | C. | D. |